   
(1)立体視とは
3次元的な物体を2次元平面上に描いて,
その2次元平面の図形から元の3次元物体を
再構成して視ることを立体視といいます。
通常は,左目で見える図形と右目で見える図形を
別々に見ることで立体視します。
ステレオカメラで写した写真を,
ステレオスコープで見ることも立体視のひとつです。
漫画等の世界では,以下のような色眼鏡を使って,
立体視することもあります。
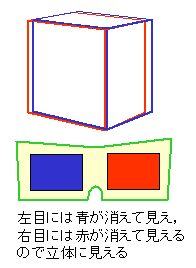
これは,
青いフィルムを通して見ると青色が消え,赤色のところだけが見え,
赤いフィルムを通してみると赤色が消え,青色のところだけが見える
ことを利用したものです。
   
(2)ランダムドット・ステレオグラムとは
ランダムドット・ステレオグラムとは1枚の図で
立体視が可能な絵のことです。
3次元図形上のランダムな点に対して,
左目で見える箇所と右目で見える箇所に
点が描かれている絵ですが,
焦点をずらしてこの絵を見ると立体に見えます。
ここでは,この絵を描くプログラムを示します。
プログラム中では,
見えている物体面が紙面に対して平行であると仮定し,
ある基準となる面から物体面の距離をdとして,
紙面上の間隔Tを以下の式で近似しています。
T=C−R・d
ここで,C:物体が基準となる位置にある場合に対応する
紙面上の点の間隔, R:ずらすための定数(値が大きいとき,
飛び出し方や引っ込み方が大きくなる)です。
   
(3)ランダムドット・ステレオグラムの見方
ランダムドット・ステレオグラムの上方に,
以下の(a)のような2つの点があります。

目をリラックスさせた状態で紙面に視線を向け,
平行法の場合は,紙面より先のほうへ,
交差法の場合は,紙面より手前のほうに
焦点を合わせるように見ると,これがぼやけて見えます。
ぼやけた円が2個,中央にはっきりした円が1個に見えるように
目の焦点をずらすと((b)の状態),ステレオグラムが立体に見えてきます。
経験のない方は,以下の例でやってみましょう。
この例は,後で示すプログラムで描いたものです。
[例1]
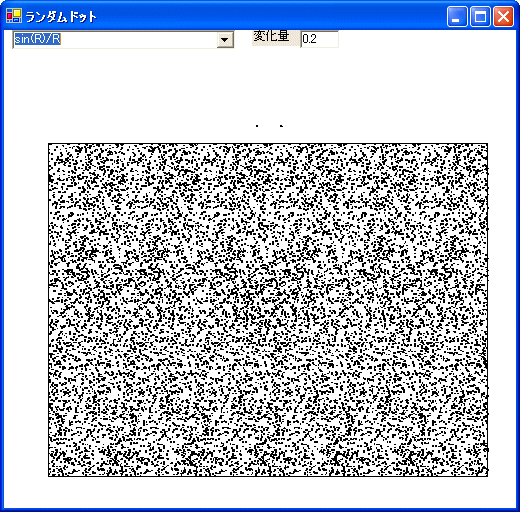
[例2]
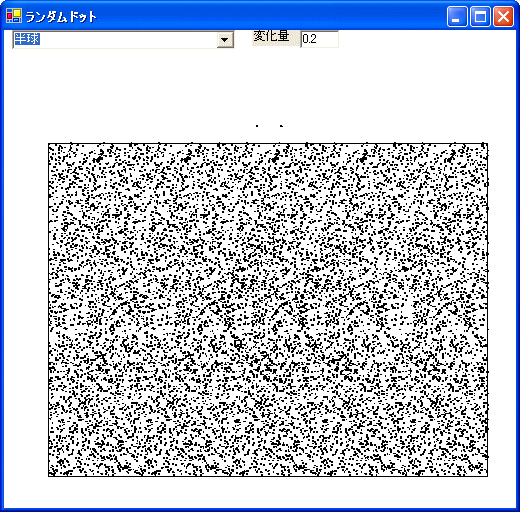
[例3]
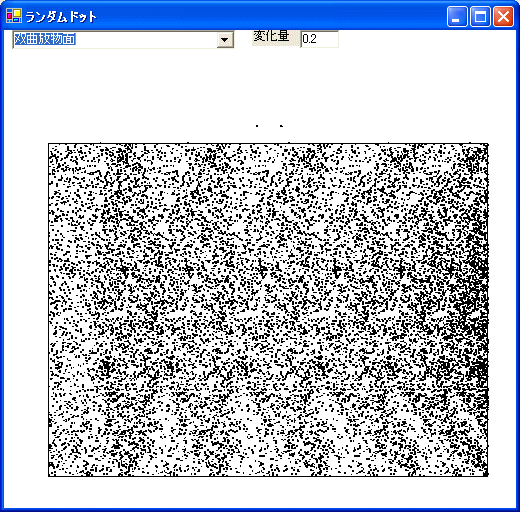
   
(4)プログラムの説明
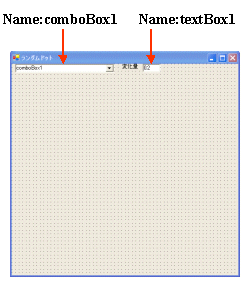
■フォームの定義
フォーム内のコントロールは,以下のように定義します。
■プログラム
2次元の絵を描くことになりますので,
以下のusingを追加しておきます。
using System.Drawing.Drawing2D;
以下のようにデータを宣言します。
public Matrix matrix =new Matrix();
public string 処理;
表示するための関数を各種揃えます。
これらの関数は,XY座標を渡したらZ座標値を返すようにします。
もし,追加したい関数があれば自由に追加しましょう。
(各種関数その1)
private double SinR_dev_R(double X, double
Y)
{
double R = Math.Sqrt(X*X+Y*Y);
if(R<=0.0000001) return 1.0;
return Math.Sin(R)/R;
}
private double 半球(double X, double
Y)
{
double R = Math.Sqrt(X*X+Y*Y);
if(R>5) return -1.0;
else { R=R/5; return Math.Sqrt(1-R*R)-1;}
}
private double 円筒(double X, double
Y)
{
double R = Math.Abs(X);
if(R>5) return -1.0;
else { R=R/5; return Math.Sqrt(1-R*R)-1;}
}
private double ピラミッド(double
X, double
Y)
{
double XX = Math.Abs(X); double R
= Math.Abs(Y);
if(XX>R) R=XX; if(R>5) return
-1;
else { R=R/2.5; return 1 -
R; }
}
private double fmod(double D, double
M)
{ return D- (int)(D/M)*M; }
private double 上下開き(double
X, double
Y)
{
double R = Math.Sqrt(X*X+Y*Y);
if(R>=10) return 0;
else if (fmod(R, 4.0)>2.0) return
Y/10;
else return -Y/10;
}
private double 双曲放物線(double
X, double
Y)
{ return (X*X-Y*Y)/50;}
private double 二次錘面(double X, double
Y)
{ return 1- Math.Sqrt(X*X+Y*Y)/5;}
private double 十字(double X, double
Y)
{
double XX=Math.Abs(X) ;
double YY=Math.Abs(Y);
if (XX>5 || YY>5) return -1;
else if(XX<1 || YY<1) return
1;
else return -1;
}
private double Def_Exp(double X, double
Y)
{
double XX=X/5 ; double YY=Y/5;
double R=XX*XX+YY*YY;
return (XX-YY) *Math.Exp(-R);
}
private double mult_R(double X, double
Y)
{
double XX=fmod(X,4)-2 ; double YY=fmod(Y,4)-2;
double R=Math.Sqrt(XX*XX+YY*YY);
if (R>1) return 0;
else return Math.Sqrt(1-R*R);
}
private double func10(double X,
double
Y)
{ return (Math.Cos(X/1.5)+Math.Sin(Y/1.5))/2;}
private double func11(double X, double
Y)
{
double XX=X/3 ; double YY=Y/3;
if( XX>0) XX=-XX;
if(YY>0) YY=-YY;
return Math.Exp(XX+YY)*2-1;
}
指定されている関数を呼出します。
private double 関数呼出(double X, double
Y)
{
int ID=comboBox1.SelectedIndex;
switch(ID)
{
case 0:return SinR_dev_R(X,Y);
case 1:return 半球(X,Y);
case 2:return 円筒(X,Y);
case 3:return ピラミッド(X,Y);
case 4:return 上下開き(X,Y);
case 5:return 双曲放物線(X,Y);
case 6:return 二次錘面(X,Y);
case 7:return 十字(X,Y);
case 8:return Def_Exp(X,Y);
case 9:return mult_R(X,Y);
case 10:return func10(X,Y);
case 11:return func11(X,Y);
}
return 0;
}
ドット表示の本体です。
public void ドット表示(PaintEventArgs
e)
{
double X1 = -12; double X2
= 12;
double Y1 = 10; double Y2 = -10;
double R0 = double.Parse(textBox1.Text);
double UNIT = 6; double XY
=1; int
Loop=3000;
double Period=(X2-X1)/6; double Z0=R0*Period;
double R, X, Y, Z;
Pen pen = new Pen(Color.Black,0.001F);
Brush brush =new SolidBrush(Color.Black);
e.Graphics.Clear(Color.White);
float XX=(float)(Period/6.0);float
YY=(float)(Y1*1.1);
e.Graphics.DrawEllipse(pen, -XX,
YY, 0.1F, 0.1F);
e.Graphics.DrawEllipse(pen, XX, YY,
0.1F, 0.1F);
Random RD = new Random();
for(int i=0;i<Loop;i++)
{
R=RD.NextDouble(); Y=R*(Y2-Y1)+Y1;
Z=関数呼出(X1,Y);
R=RD.NextDouble();
X=(Period + Math.Abs(Z0*Z))*R+X1;
while(X<=X2)
{
double XP=(X - (X1+X2)*0.5)*UNIT;
double YP=(Y - (Y1+Y2)*0.5)*UNIT;
e.Graphics.FillRectangle(brush,(float)(X-0.025),
(float)(Y-0.025),0.1F,0.1F);
Z = 関数呼出(X + Period *
0.5, Y);
X = X + Period - XY
* Z0
* Z;
}
}
}
以下は,OnPaint のオーバーライドです。
protected override void OnPaint(PaintEventArgs
e )
{
base.OnPaint(e );
e.Graphics.Clear(Color.White);
e.Graphics.Transform = matrix;
if (処理!="")ドット表示(e);
Pen pen = new Pen(Color.Black,0.001F);
e.Graphics.Transform = matrix;
e.Graphics.DrawLine(pen, -12F, 10F,12F,
10F);
e.Graphics.DrawLine(pen, -12F,-10F,12F,-10F);
e.Graphics.DrawLine(pen, -12F,10F,-12F,-10F);
e.Graphics.DrawLine(pen, 12F,10F,
12F,-10F);
}
コンボボックスが選択されたら,絵を書き直します。
private void comboBox1_SelectedIndexChanged
(object
sender,
System.EventArgs e)
{ 処理="Exe"; this.Invalidate();
}
座標変換マトリックスを設定します。
private void window(float X1, float
Y1,
float X2, float Y2)
{
float W= this.Width; float H=this.Height;
float SX=W/(X2-X1); float SY=H/(Y2-Y1);
matrix.Scale(SX,SY); matrix.Translate(-X1,-Y1);
}
Form1がロードされた際,初期設定を行います。
private void Form1_Load(object
sender,
System.EventArgs e)
{
処理="";
window(-12F*1.2F, 12F*1.4F, 10F*1.4F,-10F*1.4F);
comboBox1.Items.Clear();
comboBox1.Items.Add("sin(R)/R");
comboBox1.Items.Add("半球");
comboBox1.Items.Add("円筒");
comboBox1.Items.Add("ピラミッド");
comboBox1.Items.Add("上下開き");
comboBox1.Items.Add("双曲放物面");
comboBox1.Items.Add("二次錘面");
comboBox1.Items.Add("十字");
comboBox1.Items.Add("(x-y)exp(-(x*x+y*y))");
comboBox1.Items.Add("繰返し");
comboBox1.Items.Add("cos(x)+sin(y)");
comboBox1.Items.Add("exp(-(abs(x)+abs(y))");
comboBox1.SelectedIndex=0;
}
   
 1. 基本的なアルゴリズム 1. 基本的なアルゴリズム
 2. 基本的なデータ構造 2. 基本的なデータ構造
 3. 操作を伴うデータ構造 3. 操作を伴うデータ構造
 4. 探索 4. 探索
 5. 再帰的アルゴリズム 5. 再帰的アルゴリズム
 6. ソート 6. ソート
 7. 集合 7. 集合
 8. 文字列処理 8. 文字列処理
 9. 色々なアルゴリズム 9. 色々なアルゴリズム

上のタイトルをクリックします
|

 9.4 ランダムドット
9.4 ランダムドット




