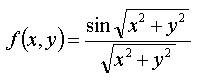(1)考え方
等高線は,3次元形状を数値的に
正確に表示するという意味では有効ですが,
直感的に図形を把握するのが困難です。
そこで,普段,見慣れた形で表示することを試みましょう。
もっとも簡単には,曲線のXYZ座標を
2次元に平行投影して表示すると良いでしょう。
以下の例は,
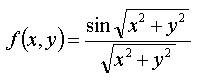
のデータを平行投影した図です。
このような表示方法をワイヤーフレーム表示と呼びます。
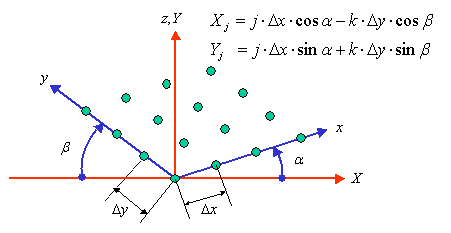
平行投影は,次のような式で変換することができます。
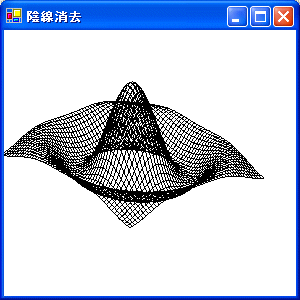
しかし,隠れた線まで表示されています。
そこで,見えない線を消すと,より見やすくなるはずです。
この見えない線を消すことを陰線消去と呼びます。
以下は,陰線消去を行った結果です。
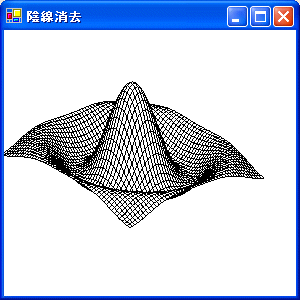
ここで示す方法は,浮動水平線アルゴリズムまたは
最大最小法と呼ばれる方法です。
その手順の概略は,以下のとおりです。
(a) 一番,手前から描く。
(b) 現在描いている曲線の1点のY座標が,
それ以前に描かれた曲線の最大Y座標値より大きければ,
(水平線より上に位置すれば),
その点が見えるものとして描きます。
すなわち,以下のように手前から順に,描きますが,
実線の部分は,先に描かれた2次元変換後のY座標より
大きいので描かれ,点線の部分は小さいので描きません。
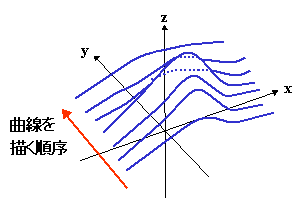
描画の進行に伴って,
水平線がYの正の方向に上がっていきますので,
浮動水平線アルゴリズムと呼ばれます。
   
(2)プログラムの説明
2次元の絵を描くことになりますので,
以下のusingを追加しておきます。
using System.Drawing.Drawing2D;
以下はデータ領域の宣言です。
public double Hidden_dlx; // 表示刻み幅(dl)
public double Hidden_alpha; // x軸と水平軸との角度(α)
public double Hidden_beta; // y軸と水平軸との角度(β)
public double Hidden_dx; // x軸方向の単位メッシュの長さ(dx)
public double Hidden_dy; // y軸方向の単位メッシュの長さ(dy)
public double[,] 高さ=new double[51,51];
//
高さ(z値)
public double[] YMax=new double[2000];
//
Y座標値の最大値(上の浮動水平線)
public double[] YMin=new double[2000];
//
Y座標値の最小値(下の浮動水平線)
public double Hidden_Xlen; // 表示上のX方向長さ=(numX-1)*dx*cos(α)
public double Hidden_Ylen; // 表示上のX方向長さ=(numY-1)*dx*cos(β)
public int Hidden_NR; // 浮動水平線用配列の長さ
public double beforX; //
現在ペン位置X
public double beforY; //
現在ペン位置Y
public int numX=51; // x方向メッシュ数
public int numY=51; // y方向メッシュ数
public double Hidden_dxCosA; // dx*cos(α)
public double Hidden_dyCosB; // dy*cos(β)
public double Hidden_dxSinA; // dx*sin(α)
public double Hidden_dySinB; // dy*sin(β)
public double Hidden_dlxTanA; // dl*tan(α)
public double Hidden_dlxTanB; // dl*tan(β)
public Matrix matrix= new Matrix();
// グローバル座標系への変換マトリックス
以下は,陰線消去の処理です。
public bool Hidden_Draw(PaintEventArgs
e,Pen pen,
double px,double py, int p, bool
Visible, bool Update)
{
// 陰線かどうかを判断し,陰線でない場合,線を描く。
//
// 関数値 : 表示後の可視フラグ
// e : 描画用引数
// pen : ペン属性
// px : 補間されたX座標値(平面座標系)
// py : 補間されたY座標値(平面座標系)
// p : 比較する浮動水平線の位置
// Visible : 現ペン位置が見えているかどうかを示すフラグ(可視フラグ)
// Update : 陰線でないとき,浮動水平線を更新するかどうかを示すフラグ
if((py>=YMax[p])||(py<=YMin[p]))
{
if(Update && py >=YMax[p])YMax[p]=py;
if(Update && py <=YMin[p])YMin[p]=py;
if(Visible)
{
float fx1=(float)beforX;
float fy1=(float)beforY;
float fx2=(float)px ;
float fy2=(float)py;
e.Graphics.DrawLine(pen,fx1,fy1,fx2,fy2);
}
beforX=px;beforY=py; return
true;
}
else{ beforX=px;beforY=py; return
false;
}
}
以下は,OnPaintのオーバライドです。
ここでは,OnPaintで直接表示していますが,
効率よく表示するには,等高線プログラムの方法,
すなわち,Imageクラスの変数に描画し,
OnPaintでは,DrawImageで表示するほうが良いでしょう。
protected override void OnPaint(PaintEventArgs
e )
{
bool 可視フラグ=true;
base.OnPaint(e);
e.Graphics.Clear(Color.White);
Pen pen=new Pen(Color.Black,0.02F);
e.Graphics.Transform=matrix;
for (int j=0;j<Hidden_NR;j++)
{
YMax[j]=-1E20; YMin[j]=1E20;}
// 浮動水平線の初期化
double X0=80; //
表示始点位置
double Y0=100;
for(int k=0;k<numY;k++)
{
可視フラグ=false;
for(int j=0;j<numX-1;j++)
{ // X軸方向描画
int p1=(int)((0.5+(Hidden_Ylen
+Hidden_GroundX(j,k))
/Hidden_dlx));
int p2=(int)((0.5+(Hidden_Ylen
+Hidden_GroundX(j+1,k))/Hidden_dlx));
for(int p=p1; p<=p2;p++) //
補間
{
double PH=(double)(p-p1);
double fp = 高さ[j,k] + (高さ[j+1,k]-高さ[j,k])
* PH * Hidden_dlx / Hidden_dxCosA;
double px = PH*Hidden_dlx
+ Hidden_GroundX(j,k)+ X0;
double py = PH*Hidden_dlxTanA
+
Hidden_GroundY(j,k) + fp + Y0;
if((j<numX-2 &&
p<p2) || (j == numX-2))
可視フラグ=Hidden_Draw(e,
pen, px, py, p,可視フラグ, true);
}
}
for(int j=0;j<numX &&
k<numY-1;j++)
{ // Y軸方向描画
可視フラグ=false;
int p1=(int)((0.5+(Hidden_Ylen
+Hidden_GroundX(j,k))
/Hidden_dlx));
int p2=(int)((0.5+(Hidden_Ylen
+Hidden_GroundX(j,k+1))/Hidden_dlx));
for(int p=p1; p>=p2;p--)
// 補間
{
double PH=(double)(p-p1);
double fp=高さ[j,k]-(高さ[j,k+1]-高さ[j,k])
*PH*Hidden_dlx/Hidden_dyCosB;
double px = PH*Hidden_dlx
+ Hidden_GroundX(j,k) + X0;
double py =-PH*Hidden_dlxTanB
+
Hidden_GroundY(j,k)
+ fp + Y0;
可視フラグ=Hidden_Draw(e,
pen, px, py, p,可視フラグ, p!=p2);
}
}
}
}
以下の関数で,X0=Y0=0の2次元座標値を求めます。
private double Hidden_GroundX(int
j,
int k) // X0=Y0=0のときのX座標
{ return (double)j * Hidden_dxCosA
-
(double) k * Hidden_dyCosB;}
private double Hidden_GroundY(int
j,
int k)// X0=Y0=0のときのY座標
{ return (double)j * Hidden_dxSinA
+
(double) k * Hidden_dySinB; }
変換マトリックスを設定します。
private void window(double X1,
double
Y1, double X2, double Y2)
{
float W=this.ClientSize.Width;
float H=this.ClientSize.Height;
float SX=W/((float)(X2-X1));
float SY=H/((float)(Y2-Y1));
matrix.Scale(SX,SY);
matrix.Translate(-(float)X1,-(float)Y1);
}
各変数の初期化を行います。
高さ[j,k]に設定する値を変えて,
色々な3次元データを表示してみましょう。
private void Form1_Load(object
sender,
System.EventArgs e)
{
double DNX2= ((double)numX)/2;
double DNY2= ((double)numY)/2;
double X,Y,R,fxy;
// 高さデータの設定
for(int j=0; j<numX; j++)
{
X=0.3*((double)j-DNX2);
for(int k=0; k<numY;
k++)
{
Y=0.3*((double)k-DNY2);
R=Math.Sqrt(X*X+Y*Y);
if(R==0.0) fxy=1.0;
else
fxy=Math.Sin(R)/R;
高さ[j,k]=40.0*fxy;
}
}
// 表示用パラメータの設定
Hidden_dlx = 0.1;
Hidden_alpha = Math.PI/12;
Hidden_beta = Math.PI/8;
Hidden_dx = 2; Hidden_dy =
1.4;
// 計算に用いる値の設定
Hidden_dxCosA=Hidden_dx*Math.Cos(Hidden_alpha);
Hidden_dyCosB=Hidden_dx*Math.Cos(Hidden_beta);
Hidden_dxSinA=Hidden_dx*Math.Sin(Hidden_alpha);
Hidden_dySinB=Hidden_dx*Math.Sin(Hidden_beta);
Hidden_Xlen=(numX-1)*Hidden_dxCosA;
Hidden_Ylen=(numY-1)*Hidden_dyCosB;
Hidden_dlxTanA=Hidden_dlx*Math.Tan(Hidden_alpha);
Hidden_dlxTanB=Hidden_dlx*Math.Tan(Hidden_beta);
Hidden_NR=(int)((Hidden_Xlen+Hidden_Ylen)/Hidden_dlx)+1;
// 表示座標マトリックスの設定
window(-10,200,200,60);
}
   
 1. 基本的なアルゴリズム 1. 基本的なアルゴリズム
 2. 基本的なデータ構造 2. 基本的なデータ構造
 3. 操作を伴うデータ構造 3. 操作を伴うデータ構造
 4. 探索 4. 探索
 5. 再帰的アルゴリズム 5. 再帰的アルゴリズム
 6. ソート 6. ソート
 7. 集合 7. 集合
 8. 文字列処理 8. 文字列処理
 9. 色々なアルゴリズム 9. 色々なアルゴリズム

上のタイトルをクリックします
|

 9.3 陰線消去
9.3 陰線消去