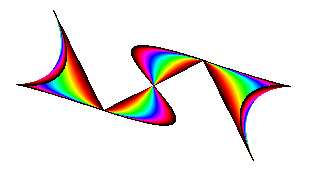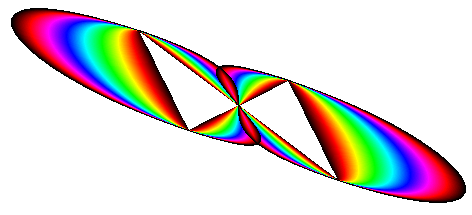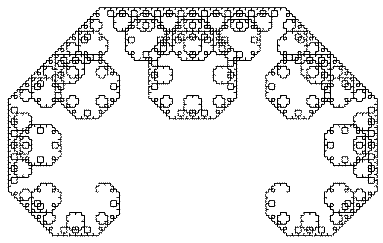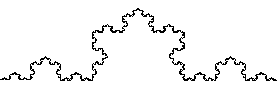(1)スプライン曲線とベジェ曲線
GraphicsクラスのDrawCurveメソッドや
DrawBezierメソッドを使うと
スプライン曲線や,ベジェ曲線を描くことができます。
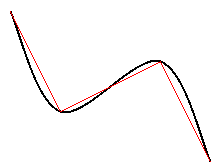 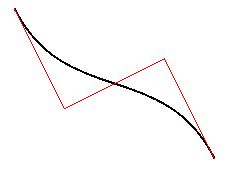
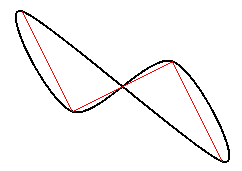
スプライン曲線では,閉曲線も描くことができます。
さらにメソッドにテンションを引数で受け渡すことで,
歪曲度を変更することができます。
 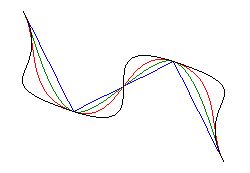
以下の例は,テンションを連続的に変化させ,
テンションの値によって線の色を変えたものです。
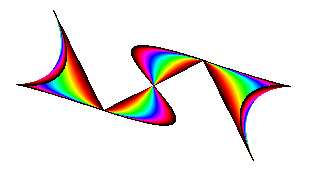 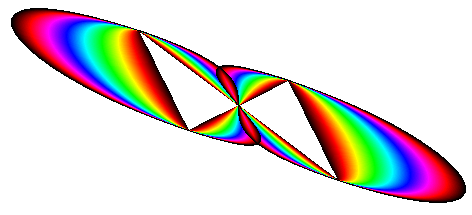
[確認用プログラム]
2次元図形を描画しますので以下のUsingを追加します。
using System.Drawing.Drawing2D;
以下は,データ宣言です。
private string 曲線="ベジェ曲線";
private Point[] 構成点={ new Point(200,100),new
Point(250,200),
new
Point(350,150),
new Point(400,250)};
private Pen pen1 = new Pen(Color.Black,2);
private Pen pen2 = new Pen(Color.Blue
,1);
private Pen pen3 = new Pen(Color.Green,1);
private Pen pen4 = new Pen(Color.Red
,1);
private Pen pen5 = new Pen(Color.Black,1);
ベジェ曲線を描くには,DrawBezierメソッドを用います。
private void ベジェ曲線(PaintEventArgs
e )
{
base.OnPaint(e);
e.Graphics.DrawBezier(pen1,構成点[0],構成点[1],構成点[2],構成点[3]);
e.Graphics.DrawLines(pen4,構成点);
}
スプライン曲線を描くには,DrawCurveメソッドを用います。
private void スプライン曲線(PaintEventArgs
e )
{
base.OnPaint(e);
e.Graphics.DrawCurve(pen1,構成点);
e.Graphics.DrawLines(pen4,構成点);
}
スプライン閉曲線を描くには,DrawClosedCurveメソッドを用います。
private void 閉曲線(PaintEventArgs
e
)
{
base.OnPaint(e);
e.Graphics.DrawClosedCurve(pen1,構成点);
e.Graphics.DrawLines(pen4,構成点);
}
DrawCurveメソッドでは,以下のようにしてテンションを指定します。
private void テンション指定(PaintEventArgs
e )
{
base.OnPaint(e);
e.Graphics.DrawCurve(pen2,
構成点,
0.0F);
e.Graphics.DrawCurve(pen3,
構成点,
0.5F);
e.Graphics.DrawCurve(pen4,
構成点,
1.0F);
e.Graphics.DrawCurve(pen5,
構成点,
2.0F);
}
DrawClosedCurveメソッドでは,以下のようにしてテンションを指定します。
private void 閉曲線テンション指定(PaintEventArgs
e )
{
base.OnPaint(e);
e.Graphics.DrawClosedCurve(pen2,構成点,0.0F,FillMode.Alternate);
e.Graphics.DrawClosedCurve(pen3,構成点,0.5F,FillMode.Alternate);
e.Graphics.DrawClosedCurve(pen4,構成点,1.0F,FillMode.Alternate);
e.Graphics.DrawClosedCurve(pen5,構成点,2.0F,FillMode.Alternate);
}
テンションを連続的に変化させながら閉図形を描きます。
private void 閉図形(PaintEventArgs
e
)
{
base.OnPaint(e);
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(i,0,0));
e.Graphics.DrawClosedCurve(pen,
構成点,
(float)i *
0.5F/255F,FillMode.Alternate);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(255,i,0));
e.Graphics.DrawClosedCurve(pen,
構成点, 0.5F+(float)i *
0.5F/255F,FillMode.Alternate);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(255-i,255,0));
e.Graphics.DrawClosedCurve(pen,
構成点, 1F+(float)i *
0.5F/255F,FillMode.Alternate);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(0,255,i));
e.Graphics.DrawClosedCurve(pen,
構成点, 1.5F+(float)i *
0.5F/255F,FillMode.Alternate);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(0,255-i,255));
e.Graphics.DrawClosedCurve(pen,
構成点, 2.0F+(float)i *
0.5F/255F,FillMode.Alternate);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(i,0,255));
e.Graphics.DrawClosedCurve(pen,
構成点, 2.5F+(float)i *
0.5F/255F,FillMode.Alternate);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(255,0,255-i));
e.Graphics.DrawClosedCurve(pen,
構成点, 3.0F+(float)i *
0.5F/255F,FillMode.Alternate);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(255-i,0,0));
e.Graphics.DrawClosedCurve(pen,
構成点, 3.5F+(float)i *
0.5F/255F,FillMode.Alternate);
}
}
テンションを連続的に変化させながら開図形を描きます。
private void 図形(PaintEventArgs
e )
{ base.OnPaint(e);
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(i,0,0));
e.Graphics.DrawCurve(pen, 構成点,
(float)i * 0.5F/255F);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(255,i,0));
e.Graphics.DrawCurve(pen, 構成点,
0.5F+(float)i * 0.5F/255F);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(255-i,255,0));
e.Graphics.DrawCurve(pen, 構成点,
1F+(float)i * 0.5F/255F);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(0,255,i));
e.Graphics.DrawCurve(pen, 構成点,
1.5F+(float)i * 0.5F/255F);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(0,255-i,255));
e.Graphics.DrawCurve(pen, 構成点,
2.0F+(float)i * 0.5F/255F);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(i,0,255));
e.Graphics.DrawCurve(pen, 構成点,
2.5F+(float)i * 0.5F/255F);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(255,0,255-i));
e.Graphics.DrawCurve(pen, 構成点,
3.0F+(float)i * 0.5F/255F);
}
for(int i=0;i<255;i++)
{ Pen pen =new Pen(Color.FromArgb(255-i,0,0));
e.Graphics.DrawCurve(pen, 構成点,
3.5F+(float)i * 0.5F/255F);
}
}
OnPaintのオーバライドで各曲線のプログラムを呼び出します。
protected override void OnPaint(PaintEventArgs
e )
{
switch (曲線)
{
case "ベジェ曲線"
: ベジェ曲線(e) ;break;
case "スプライン曲線"
: スプライン曲線(e);break;
case "テンション指定"
: テンション指定(e);break;
case "図形" :
図形(e);break;
case "閉曲線"
: 閉曲線(e);break;
case "閉曲線テンション":
閉曲線テンション指定(e);break;
case "閉図形"
:
閉図形(e);break;
}
}
以下,それぞれのボタンのClickイベントハンドラです。
private void button1_Click(object
sender,
System.EventArgs e)
{ 曲線=“ベジェ曲線”; Invalidate();}
private void button2_Click(object
sender,
System.EventArgs e)
{ 曲線="スプライン曲線"
Invalidate();
}
private void button3_Click(object
sender,
System.EventArgs e)
{ 曲線="テンション指定"
Invalidate();}
private void button4_Click(object
sender,
System.EventArgs e)
{ 曲線=“図形”; Invalidate();}
private void button5_Click(object
sender,
System.EventArgs e)
{ 曲線="閉曲線" Invalidate();
}
private void button6_Click(object
sender,
System.EventArgs e)
{ 曲線=“閉曲線テンション”; Invalidate();}
private void button7_Click(object
sender,
System.EventArgs e)
{ 曲線="閉図形" Invalidate();}
  
(2)C曲線
現在位置から相対座標に至るC曲線を描くプログラムです。
最大長を小さくするとより複雑な曲線が得られます。
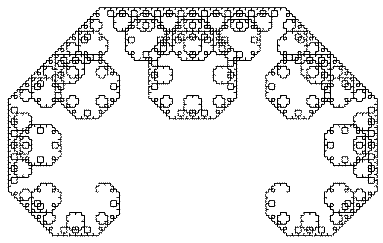
[プログラム例]
フォームには,オプション入力用として,
textBox1(開始位置X座標), textBox2(現在位置Y座標),
textBox3(最大長), textBox4(線の太さ)を用意します。
更に,button1(描画開始),button2(表示クリア)用の
コマンドボタンを用意します。
private Image image;
private Point currentPoint=new
Point();
private Point nextPoint=new Point();
private double maxLength=2;
private int lineWidth=1;
protected override void OnPaint(PaintEventArgs
e )
{
base.OnPaint(e);
e.Graphics.DrawImage(image,0,0);
}
private void drawRelative(int X,
int
Y)
{
nextPoint.X=currentPoint.X+X; nextPoint.Y=currentPoint.Y+Y;
Graphics g =Graphics.FromImage(image);
Pen pen = new Pen(Color.Black,lineWidth);
g.DrawLine(pen,currentPoint,nextPoint);
currentPoint=nextPoint;
}
private void moveAbsolute(int X,
int
Y)
{ currentPoint.X=X; currentPoint.Y=Y; }
private void C_Curve(double X,
double
Y)
{
if(X*X+Y*Y<=maxLength*maxLength)
drawRelative((int)X, (int)Y);
else
{
C_Curve((X+Y)/2,(Y-X)/2);
C_Curve((X-Y)/2,(Y+X)/2);
}
}
private void button1_Click(object sender,
System.EventArgs e)
{
Graphics g =Graphics.FromImage(image);
g.Clear(BackColor);
maxLength=double.Parse(textBox1.Text);
int X=int.Parse(textBox2.Text);
int Y=int.Parse(textBox3.Text);
lineWidth=int.Parse(textBox4.Text);
moveAbsolute(X,Y);
C_Curve(500,0);
this.Invalidate();
}
private void button2_Click(object sender,
System.EventArgs e)
{
Graphics g =Graphics.FromImage(image);
g.Clear(BackColor);
this.Invalidate();
}
  
(3)コッホ曲線
さ1の線分を三等分し,中央の1/3を削除し,
そこに1/3の長さの正三角形を挿入します。
この操作をあらたにできた辺に対して施します。
これを繰り返して得られる曲線をコッホ曲線と呼びます。
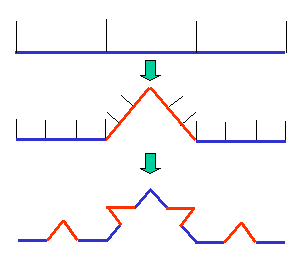
ある部分をみると,そこが更に同じ形になっていますので,
これを自己相似形と呼びます。
このようにして得られたコッホ曲線の例を以下に示します。
このような簡単な操作にも関わらず
実に複雑な形を示しています。
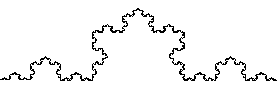
[プログラム例]
コッホ曲線のプログラム例を示す前に,
共通的なメソッドを示します。
(追加するusing)
using System.Drawing.Drawing2D;
(データ宣言)
public struct 位置データ
{ public double X; public
double
Y; }
public 位置データ 現在位置 = new
位置データ();
public double 角度;
(共通処理)
// 現在位置の設定
public void t_position(double X,
double
Y)
{ 現在位置.X=X; 現在位置.Y=Y;}
// 角度の設定
public void t_Degree(double Theta)
{ 角度=Theta; }
// 進行方向を変える
public void t_turn(double Theta)
{ 角度 += Theta; }
// 現在進行方向に指定された長さ分だけ進む
public void t_forward(PaintEventArgs
e, double length)
{ double TH = 角度 * 3.1415926/180;
double X=現在位置.X+length
* Math.Cos(TH);
double Y=現在位置.Y+length
* Math.Sin(TH);
Pen pen =new Pen(Color.Black);
e.Graphics.DrawLine(pen,
(int)現在位置.X, 300-(int)現在位置.Y,
(int)X,300-(int)Y);
現在位置.X=X; 現在位置.Y=Y;
}
コッホ曲線を描く処理は,
現進行方向に1/3だけ進み,60度方向を変える。
その方向に1/3だけ進み,-120度方向を変える。
更に1/3だけ進み,60度方向を変える。
方向は,60度→ -120度→ 60度,
すなわち,最後は最初の方向に戻ります。
以上から,以下のように再帰的に表現できます。
public void koch( PaintEventArgs
e,int
n,double length)
{
if(n<=0) t_forward(e,length);
else
{
int nn=n-1; double len=length/3;
koch(e, nn,len); t_turn(60);
koch(e, nn,len); t_turn(-120);
koch(e, nn,len); t_turn(60);
koch(e, nn,len);
}
}
  
(4)立ち枯れ木立
コッホ曲線では,長さを1/3にして,60度向きを変え,
3回再帰的呼出しを行っていますが,
これらの長さの比率,向き,呼出し回数を
色々と変えると様々な図形が得られます。
ここでは,以下のように進行方向,比率を変えてみましょう。
|
向き |
比率 |
|
0度 |
0.28 |
|
88度 |
0.28 |
|
-176度 |
0.28 |
|
88度 |
0.70 |
ここで,向きの合計が0度になっていることを確認してください。
[プログラム例]
データ宣言や共通処理は,コッホ曲線と同じです。
public double[,] element
=new double[,]{{ 0.0, 0.28},{88.0,
0.28},
{-176.0, 0.28},{88.0,
0.70}};
public void frctl( PaintEventArgs
e,
double length)
{
int j;
if (length <=2.0) t_forward(e,length);
else
{
for(j=0; j<4; j++)
{
t_turn(element[j,0]);
frctl(e, length*element[j,1]);
}
}
}
[実行例]
以下のような絵になりますので,立ち枯れ木立と呼ばれます。

皆さんも
色々と比率や方向を変えて実行してみると
面白いでしょう。
  
(5)シェルピンスキーのギャスケット
シェルピンスキーのギャスケットとは,
三角形の中に1辺の長さ1/2の三角形を
順次描くことによって得られます。
これもコッホ曲線と同様,
自己相似を内部に持つ形になります。
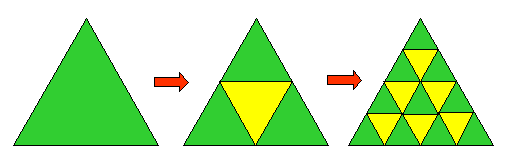
[プログラム例]
データ宣言は,コッホ曲線と同じです。
public void 三角形(PaintEventArgs
e,
double
X, double
Y, double L)
{
Pen pen =new Pen(Color.Black);
int IX1=(int)X; int IX2=(int)(X
+ L );
int IX3=(int)(X + L / 2);
int IY1=300-(int)Y;
int IY2=300-(int)(Y- L*Math.Sin(60*3.1415926/180));
e.Graphics.DrawLine(pen, IX1,IY1,
IX2,IY1);
e.Graphics.DrawLine(pen, IX1,IY1,
IX3,IY2);
e.Graphics.DrawLine(pen, IX2,IY1,
IX3,IY2);
}
public void sier( PaintEventArgs
e,
int n, double
X,
double Y, double L)
{
if(n==0) return;
double H = L * Math.Sin(60*3.1415926/180);
三角形(e, X + L / 4, Y + H
/ 2, L/2);
sier(e, n-1, X , Y , L / 2);
sier(e, n-1, X + L/2, Y , L
/ 2);
sier(e, n-1, X + L/4, Y + H
/ 2,
L / 2);
}
public void sier( PaintEventArgs
e)
{
三角形(e,290.0,10.0,-280.0);
sier(e, 6, 10.0, 10.0, 280.0);
}
[実行例]

  
(6)コッホ曲線以降の表示
上記,(3)以降については,
初期化やコマンドボタンの Click イベントハンドラ等を
示していませんでしたので,ここで提示します。
まず,フォーム定義では,button1,button2,button3を
右上に配置しておきます。
コッホのプログラムで示したデータ宣言に
以下の変数宣言を追加します。
public Matrix matrix=new Matrix();
public string 処理;
これまでに示したプログラムに
以下の記述を追加します。
protected override void OnPaint(
PaintEventArgs
e)
{
base.OnPaint(e);
e.Graphics.Clear(Color.WhiteSmoke);
Pen pen =new Pen(Color.Red);
Rectangle rect = new Rectangle(0,0,300,300);
e.Graphics.Transform=matrix;
e.Graphics.DrawRectangle(pen,
rect);
t_position(0.0,40.0);
t_Degree(0.0);
switch (処理)
{
case "" : break;
case "koch" : koch(e,
6, 300.0); break;
case "frctl": frctl(e,
300.0) ; break;
case "sier" : sier(e)
; break;
}
}
public void window(float X1,float
Y1,float
X2,float Y2, float R)
{
float W=ClientSize.Width;
float H=ClientSize.Height;
float SX=W/(X2-X1); float SY=H/(Y2-Y1);
matrix.Scale(SX,SY);
matrix.Rotate(R);
matrix.Translate(-X1,-Y1);
}
private void Form1_Load(object
sender,
System.EventArgs e)
{
処理=“”;
window(-10F,-10F,310F,310F,0);
this.Invalidate();
}
private void button1_Click(object
sender,
System.EventArgs e)
{ 処理="koch"; this.Invalidate();}
private void button2_Click(object
sender,
System.EventArgs e)
{ 処理="frctl" this.Invalidate();}
private void button3_Click(object
sender,
System.EventArgs e)
{ 処理="sier" this.Invalidate();
}
  
(7)反復関数系
自己相似図形があれば,その図形を構成する
反復関数系を見つけ,各関数に確率を割り振って,
乱数で得られた座標に点を打つことで,
色々な図形を生成できます。
もちろんシェルピンスキーのギャスケットも,
この方法で表現できます。
ここでは,別の例を示しますので,
シェルピンスキーのギャスケットについては,
皆さんでチャレンジしてみてください。
なお,フラクタル図形の教科書を参照するのも
ひとつの手段でしょう。
ここでは,以下のような反復関数系を実行してみます。
ⅰ)反復関数系

ⅱ)発生確率
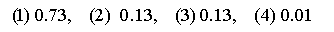
ⅲ)実行例

[プログラム例]
(追加するusing)
using System.Drawing.Drawing2D;
(データ宣言)
public double [,,] Fsys1=new double[,,]
{{{ 0.856, 0.0414}, {-0.0205,
0.858}},
{{ 0.244,-0.3850}, { 0.1760,
0.224}},
{{-0.144, 0.3900}, { 0.1810,
0.259}},
{{ 0.000, 0.0000}, { 0.3550,
0.216}}};
public double [,] Fsys2 = new double
[,]
{{0.07,0.147},{0.393,0.102},{0.527,-0.014},{0.486,0.05}};
public bool[,] 点=new bool[1001,1001];
public Matrix matrix=new Matrix();
private Image image;
(描画処理)
public void 描画()
{
Brush brush = new SolidBrush(Color.DarkGreen);
Graphics g=Graphics.FromImage(image);
g.Clear(Color.White);
for(int i=0; i<1000; i++)
for(int j=0; j<1000;
j++)
if(点[i,j]) g.FillRectangle(brush,i,(1000-j),1,1);
}
protected override void OnPaint(PaintEventArgs
e)
{
base.OnPaint(e);
e.Graphics.Transform=matrix;
e.Graphics.DrawImage(image,100,100);
}
(変換マトリックス設定)
private void window(float X1,float
Y1,float
X2, float Y2, float R)
{
float W =ClientSize.Width;
float H=ClientSize.Height;
float SX=W/(X2-1); float SY
= H /
(Y2 -Y1);
float MX= -SX *X1; float MY
= - SY
* Y1;
matrix.Scale(SX,SY); matrix.Rotate(R);
matrix.Translate(MX,MY);
}
(初期化)
private void 初期化()
{
for(int i=0; i<1001; i++)
for(int j=0; j<1001;
j++)
点[i,j]=false;
描画();
}
private void Form1_Load(object
sender,
System.EventArgs e)
{ 初期化(); window(0,0,1000,1000,0);}
(ボタンClick処理)
private void button1_Click(object
sender,
System.EventArgs e)
{
int ID;double X1,Y1;
Random RD = new Random();
double X0=1.0; double Y0=1.0;
for(int i=0; i<20000; i++)
{
double R=RD.NextDouble();
if (R < 0.73) ID = 0;
else if (R < 0.86) ID
= 1;
else if (R < 0.99) ID
= 2;
else ID = 3;
X1=Fsys1[ID,0,0]*X0+Fsys1[ID,0,1]*Y0+Fsys2[ID,0];
Y1=Fsys1[ID,1,0]*X0+Fsys1[ID,1,1]*Y0+Fsys2[ID,1];
if(X1<1.0 &&
Y1<1.0
&& X1>=0 && Y1>=0)
点[(int) (X1*1000.0),(int)
(Y1*1000.0)]=true;
X0=X1;Y0=Y1;
}
描画(); this.Invalidate();
}
  
 1. 基本的なアルゴリズム 1. 基本的なアルゴリズム
 2. 基本的なデータ構造 2. 基本的なデータ構造
 3. 操作を伴うデータ構造 3. 操作を伴うデータ構造
 4. 探索 4. 探索
 5. 再帰的アルゴリズム 5. 再帰的アルゴリズム
 6. ソート 6. ソート
 7. 集合 7. 集合
 8. 文字列処理 8. 文字列処理
 9. 色々なアルゴリズム 9. 色々なアルゴリズム

上のタイトルをクリックします
|

 9.5 色々な曲線/フラクタル
9.5 色々な曲線/フラクタル