  
（１）末尾再帰
関数の最後で呼び出される再帰呼出しを
末尾再帰（tail recursion）といいます。
末尾再帰の場合，再帰呼び出しは簡単に除去できます。
再帰除去の前に，
階乗の計算の再帰呼び出しを観察してみましょう。
引数ｎの値は，呼び出すたびに１ずつ減算されて，
最終的に0になります。
引数の値が0になると，リターン値が１になります。
リターンするたびに，それぞれの段階のｎの値を乗じます。
すなわち，初期値を１にして１からｎまでを乗じることになります。
これをプログラムに直すと，以下のようになります。
private long fact2(long n)
{
long r=1;
for(long i=1;i <= n;i++) r *=
i;
return r;
}
（２）真に再帰的な場合
２回以上再帰呼び出しを行う関数を真に（genuinely）再帰的であるといいます。
真に再帰的な関数の動きを見るために，次のプログラムを例にとってみましょう。
private void test(int n)
{
if(n <= 0 ) return;
test(n - 1);
MessageBox.Show(n.ToString());
test(n - 2);
}
このプログラムは，特に意味のある処理ではありませんが，
再帰的な動きを観察することができるようにしたプログラムです。
引数を４として呼び出すと，次の青矢印のように呼び出しが行われ，
赤矢印のようにリターンします。
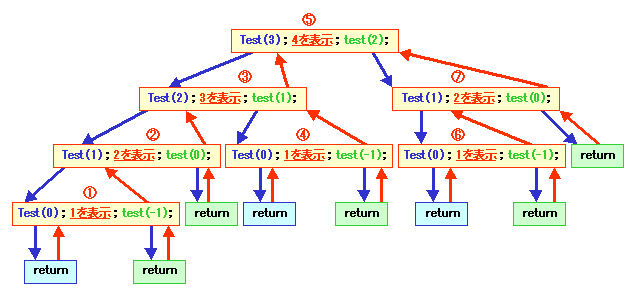
表示は，赤丸数字の順，すなわち
１，２，３，１，４，１，２
の順に表示されます。
以前出てきた，２分木の場合の通りがけ順と同じような表示順序になっています。
（３）再帰的プログラムのループ化
末尾再帰は，簡単にループ化できますが，以下の下線部は再帰のまま残ってしまいます。
private void test(int n)
{
int nn = n;
while (nn > 0 )
{
test(nn - 1);
MessageBox.Show(nn.ToString());
nn = nn - 2;
}
}
一般に，再帰的なプログラムを形式的にループ化するには，スタックを使います。
（２）の図の左側に進むときは，現在の値をスタックに積み，１ずつ減じます。
０以下になったら，スタックをポップ（リターン処理）してその値を表示します。
スタックが空になっているときは，終わらせます。
右側に進むときは，末尾再帰ですから，ｎを2だけ減じて繰返します。
private void test(int n)
{
int[] stk = new int[20];
int p = 0; int nn = n;
bool flag = true;
while(flag) //
継続するときtrue
{
while (nn > 0 ) { stk[p++]
= nn; nn = nn - 1; }
if(p == 0) flag = false; //
スタック空のとき停止
else
{
nn = stk[--p];
MessageBox.Show(nn.ToString());
nn = nn - 2;
}
}
}
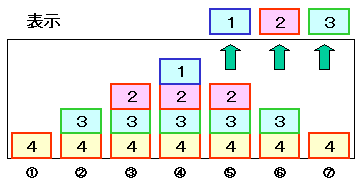
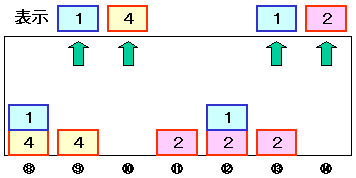
呼出しtest(4)のときのスタック状態を以下に示します。
i
 1. 基本的なアルゴリズム
2. 基本的なデータ構造
3. 操作を伴うデータ構造
4. 探索
5. 再帰的アルゴリズム
6. ソート
7. 集合
8. 文字列処理
9. 色々なアルゴリズム
上のタイトルをクリックします
|
5．2 再帰的プログラムの動き