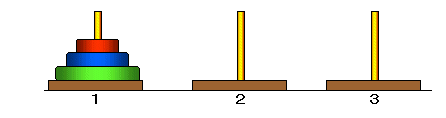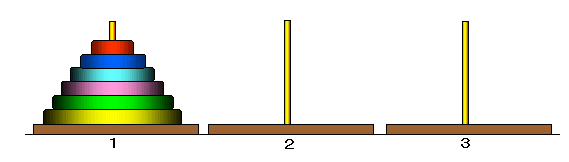  
（１）ハノイの塔とは
ハノイの塔とは，重なった円盤を３本柱の間で移動する問題です。
ただし，より小さい円盤が必ず上にくるように重ねます。
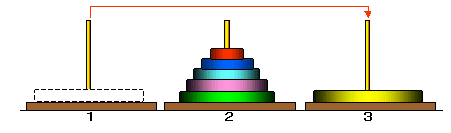
たとえば，3枚の円盤の場合，以下のように，
一番左の柱（番号：１）に3枚の円盤があったとします。
これを一番右（番号：３）の柱に移します。
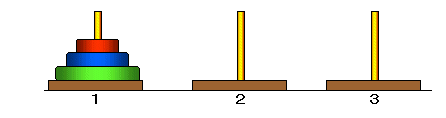
（２）3枚の場合の手順
たとえば，3枚の場合，次のような手順で1番の柱から3番の柱に移動することができます。
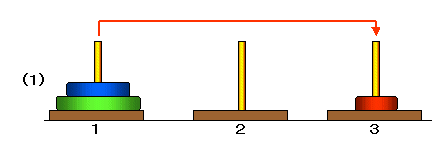
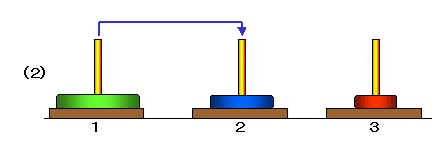
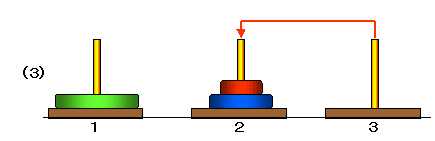
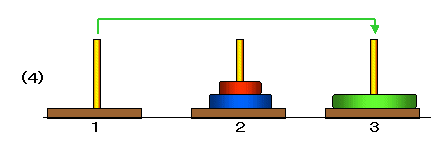
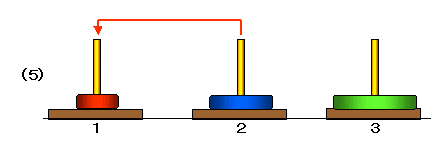
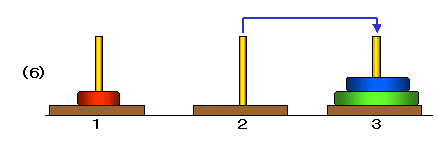
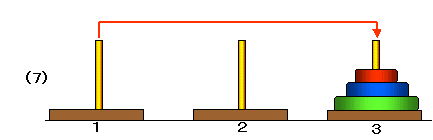
ここで，
■ （１）から（３）は，2枚の円盤を塔１から塔２に移動する手順，
■ （４）は，最も大きい円盤を塔１から塔３に移動，
■ （５）から（７）は，2枚の円盤を塔２から塔３に移動する手順
です。
（３）Ｎ枚の場合の手順
3枚の場合を一般化することを試みましょう。
移動前の塔をＡ，移動先の塔をＢ，残りの塔をＣとすると，
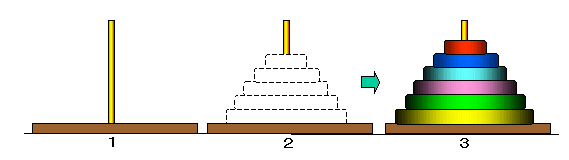
■ ＡからＣにＮ−１枚を移動
■ ＡからＢに1枚を移動
■ ＣからＢにＮ−１枚を移動
とすることができます。
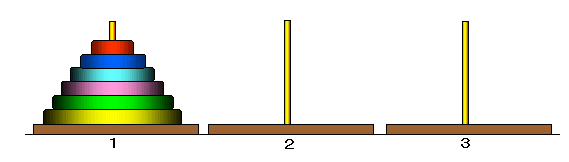
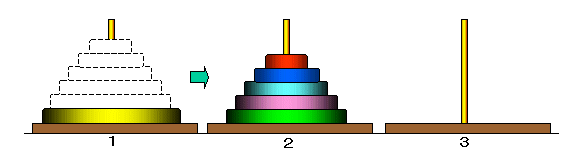
Ａ，Ｂの組合せに対するＣは，次の表の通りとなります。
| A |
B |
C |
A+B+C |
| 1 |
2 |
3 |
6 |
| 1 |
3 |
2 |
6 |
| 2 |
3 |
1 |
6 |
| 2 |
1 |
3 |
6 |
| 3 |
1 |
2 |
6 |
| 3 |
2 |
1 |
6 |
表に示すとおり，
A+B+C=6
の関係が成り立ちますから，
C = 6-(A+B)
とすることができます。
［プログラム例］
フォーム上に，textBox1，listBox1，button1を貼り付け，
枚数をtextBox1で指定して，button1をクリックしたら，
ｌistBox1に手順が表示されるものとします。
private void MoveTo(int n,int x, int
y)
{
string S=“第”+ n.ToString()
+ “盤を”
+
x.ToString() +
“軸から”
+
y.ToString() +
"に移動";
listBox1.Items.Add(S);
}
private void Hanoi(int n, int x,
int
y)
{
if(n>0) //
0 枚のときは何もしない
{
Hanoi(n-1,x, 6-x-y); //
n - 1 枚を x → 中間的な塔
MoveTo(n,x,y);
//
最も大きい円盤を x → y
Hanoi(n-1,6-x-y, y); //
n - 1 枚を 中間的な塔 → y
}
}
private void button1_Click(object
sender,
System.EventArgs e)
{
listBox1.Items.Clear();
int n = int.Parse(textBox1.Text);
Hanoi(n,1,3);
}
i
 1. 基本的なアルゴリズム
2. 基本的なデータ構造
3. 操作を伴うデータ構造
4. 探索
5. 再帰的アルゴリズム
6. ソート
7. 集合
8. 文字列処理
9. 色々なアルゴリズム
上のタイトルをクリックします
|
5．3 ハノイの塔