 
（１）再帰的定義
ある事象が，自分自身を含んでいたり，
それを用いて定義されていることを，
再帰的（recursive）
といいます。たとえば，自然数は，
（a）１は自然数である。
（b）ある自然数の直後の整数は自然数である。
と再帰的に定義されますが，このような定義を
再帰的定義（recursive definition）
といいます。
（２）再帰的定義の例
操作を伴うデータ構造で出てきた木構造の探索は，
再帰的な問題の代表例です。
もっとも簡単な２分木の探索方法は，
@）自ノードと等しければ探索完了
A）左部分木を探索
B）右部分木を探索
として，左部分木，右部分木も２分木ですから，
再帰的な問題となります。
［木構造について復習するには，こちらから］
いわゆる数学的帰納法で定義されるような問題も，
再帰的な問題となります。
たとえば，階乗値を求める数学的帰納法による定義
@） f(0) = 1
A） n > 0に対して f(n) = n
× f（n−1）
は，ｆ(n)を求めるのに，f(n-1)を使っています。
したがって，再帰的な問題として捉えることができます。
これをC#のプログラムとして定義すると，たとえば
private long fact(long n)
{
if(n == 0) return 1;
else return(n * fact( n -1));
}
と表現できます。
（３）再帰的プログラムの動き
再帰的なプログラムの呼出しでは，
以下のように，次々と自分自身のコピーを作って，
コピーを呼び出すと考えれば分かりやすいでしょう。
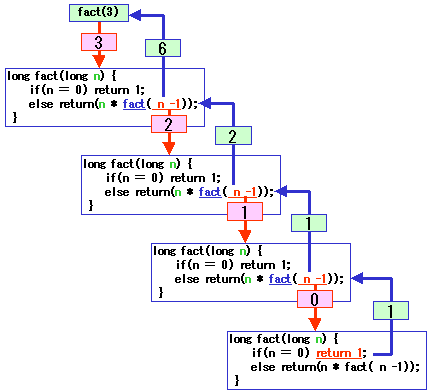
復帰する際は，自分自身を削除して，
呼び出した側に関数値を戻すという動きになります。
すなわち，再帰的な呼び出しは，
自分自身を呼び出すというよりは，
自分自身と同じ表現の関数を呼び出すとみなすほうが
分かりやすいでしょう。
（４）直接的な再帰と間接的な再帰
階乗の計算のように，自分と同じ関数を呼び出すことを
直接的な（direct）再帰といいます。
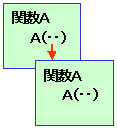
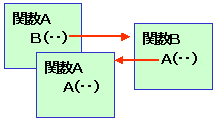
次のように，別の関数を呼出し，
その関数が自分と同じ関数を呼び出すことを，
間接的な（indirect）再帰といいます。
i
 1. 基本的なアルゴリズム
2. 基本的なデータ構造
3. 操作を伴うデータ構造
4. 探索
5. 再帰的アルゴリズム
6. ソート
7. 集合
8. 文字列処理
9. 色々なアルゴリズム
上のタイトルをクリックします
|
5．1 再帰の考え方