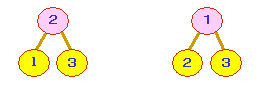(1)木構造
階層的な関係を表現する際,木構造が使われます。
木構造の各部分は,次のように木と対比できます。
ⅰ)根(root)
ⅱ)節(node)
ⅲ)枝(edge/branch)
ⅳ)葉(leaf/terminal node)
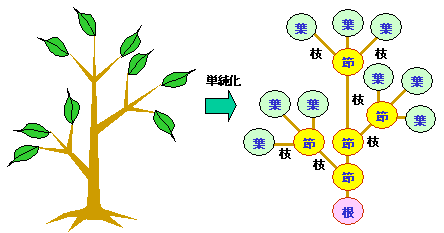
木構造は,通常,次のように上下反転した形で図示されます。
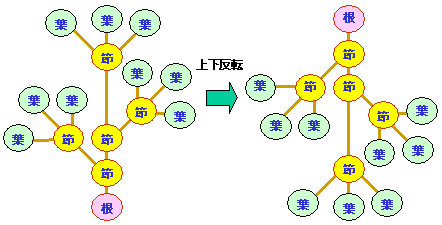
ノード間の関係を言い表す際,
ⅰ)根に近いノードを親(parent)
ⅱ)根から遠いノード/葉を子(child)
ⅲ)共通の親を持つ子を兄弟(sibling)
といいます。
いわば,葉は子を持たないノードということができます。
  
(2)順序木と無順序木
木構造のキーの取り扱い方により,木構造は次のように分類できます。
| |
ⅰ) |
順序木 |
(ordered tree) |
:兄弟関係で順序関係を持つ木
|
| |
ⅱ) |
無順序木 |
(unordered tree) |
:兄弟関係で順序関係を持たない木 |
ただし,この分類は,木構造そのものの違いではなく,
あくまで,取り扱い方法によります。
たとえば,以下の木は,順序木とみなせば異なる木であり,
無順序木とみなせば,値が異なるだけの同一の木となります。
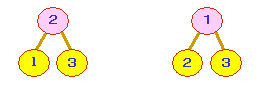
  
(3)2分木
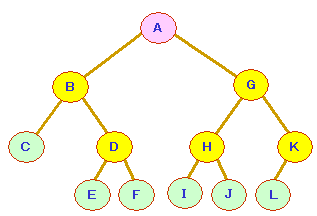
左の子(left child)と右の子(right child)の高々2つの子を持つ木を
2分木(binary tree)と呼びます。
ただし,左の子だけのノード,右の子だけのノード,
子を持たないノード(leaf/terminal node)もありえます。
  
(4)木の探索方法
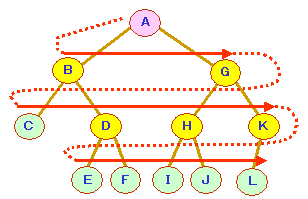
(a)横型探索/幅優先探索(breadth-first
search)
ルートに近い点から横方向に探索します。
すなわち,兄弟関係方向を優先して探索する方法です。
以下の木では,以下のような順序で探索します。
A→B→G→C→D→H→K→E→F→I→J→L
(b)縦型探索/深さ優先探索(depth-first
search)
以下のように,深さ方向を優先して探索する方法です。
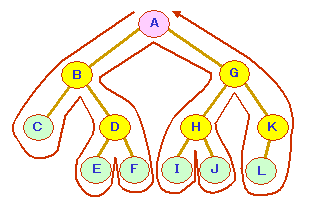
探索する際,たどり着いたノードでチェックや何らかの処理を行います。
この処理を行うタイミングで次のように分類することができます。
[3三種類のたどり方]
ⅰ)行きがけ順(ノード処理 → 左へ → 右へ)
ⅱ)通りがけ順(左へ → ノード処理 → 右へ)
ⅲ)帰りがけ順(左へ → 右へ → ノード処理)
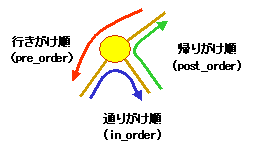
例示した2分木では,たどり方によって,
次のように処理順序が異なることになります。
ⅰ)行きがけ順:A→B→C→D→E→F→G→H→I→J→K→L
ⅱ)通りがけ順:C→B→E→D→F→A→I→H→J→G→L→K
ⅲ)帰りがけ順:C→E→F→D→B→I→J→H→L→K→G→A
  
(5)2分探索木
(a)2分探索木の定義
以下の条件を持つ2分木を,2分探索木(binary
search tree)とよびます。
ⅰ)左部分木のすべてのキー値は,対象ノードのキー値より小さい。
ⅱ)右部分木のすべてのキー値は,対象ノードのキー地より大きい。
(b)2分探索木の実装
2分探索木を実装するために,線形リストと同様,
たとえば,次のように宣言します。
public struct ElementData
{
public long 番号;
public string 氏名;
public int 点数;
}
public struct DataSet
{
public ElementData Element;
public long Left;
public long Right;
}
public DataSet[] DataArea = new
DataSet[500];
public long ErasedP;
public long DataP;
public ElementData[] tempData;
領域管理におけるフリーリストは,
便宜上,Rightポインタで連結することにします。
private void 初期設定()
{
long N = DataArea.Length - 1; long
i = 0;
while(i < N) DataArea[i].Right
= ++i;
DataArea[N].Right = -1; ErasedP
=
0;
}
private long getArea()
{
long P = ErasedP;
if(P >= 0) ErasedP = right(P);
else MessageBox.Show("領域を確保できません");
return P;
}
private void freeArea(long P)
{
if(P < 0) return;
DataArea[P].Right = ErasedP;
ErasedP = P;
}
  
(6)2分探索木の基本操作
2分木における処理は,
基本的に,次のような処理分かれます。
ⅰ)左部分木の処理
ⅱ)右部分木の処理
ⅲ)当該ノードの処理
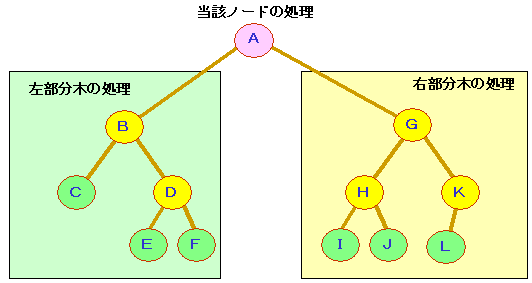
ただし,これらの処理をどの順序で行うかは,
問題が必要とするたどり方によります。
| |
ⅰ) |
行きがけ順の問題 |
: |
当該ノード→左部分木→右部分木 |
| |
ⅱ) |
通りがけ順の問題 |
: |
左部分木→当該ノード→右部分木 |
| |
ⅲ) |
帰りがけ順の問題 |
: |
左部分木→右部分木→当該ノード |
(a)要素データの取り出し
[プログラム処理]
private ElementData element(long P)
{
return DataArea[P].Element;
}
(b)右ポインタ
[プログラム処理]
private long right(long P)
{
return DataArea[P].Right;
}
(c)左ポインタ
[プログラム処理]
private long left(long P)
{
return DataArea[P].Left;
}
(d)要素数のカウント
カウントは,以下のように再帰的な処理になります。
再帰的なアルゴリズムについては5章で説明します。
加算は帰りがけ順になっています。
すなわち,
ⅰ)ポインタが空なら0個とする。
ⅱ)空でなければ,
左部分木のノード数+右部分木のノー度数+1
最後の1が当該ノードの数とみなすことができます。
[プログラム処理]
private long count(long P)
{
if(P<0) return 0;
return count(left(P))+count(right(P))+1;
}
(e)木構造すべてを開放
この処理も,再帰的な処理になります。
再帰的なアルゴリズムについては5章で説明します。
1ノードの領域開放は,帰りがけ順になっています。
すなわち,次のように処理します。
ⅰ)ポインタが空なら何もしない。
ⅱ)空でなければ,
・左部分木を開放
・右部分木を開放
・該当ノードを開放
[プログラム処理]
private void freeAll(long P)
{
if(P<0) return ;
freeAll(left(P)); freeAll(right(P));
freeArea(P);
}
(f)木を配列に移動
この処理も,再帰的な処理になります。
再帰的なアルゴリズムについては5章で説明します。
配列への移動は,通りがけ順になっています。
すなわち,次のように処理します。
ⅰ)ポインタが空なら何もしない。
ⅱ)空でなければ,
・左部分木を配列に移動
・該当ノードを配列に移動
・右部分木を配列に開放
[プログラム処理]
private long 木を配列に移動(long P, long
ID)
{
if(P<0) return ID;
long ID1 = 木を配列に移動(left(P),
ID);
tempData[ID1].番号 = DataArea[P].Element.番号;
tempData[ID1].氏名 = DataArea[P].Element.氏名;
tempData[ID1].点数 = DataArea[P].Element.点数;
ID1++;
long ID2 = 木を配列に移動(right(P),
ID1);
return ID2;
}
(g)配列を木に変換
理想的には,左の子孫のノード数と,右の子孫のノード数が等しい場合,
最も効率のよい探索が行われます。
このような木を構成する,最も単純な方法は,
キー順に並べられた配列の真ん中の値をノードとし,
左右に分け,更に左右の配列を木に変換する方法です。
この方法を以下に図示します。
黄色は中央値で,ノードになる要素,
薄青色はLeft,薄赤色はRightになる部分です。
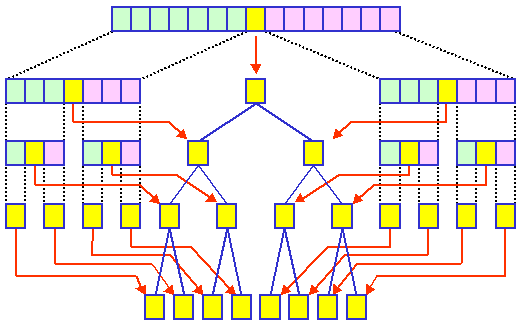
この処理も,再帰的な処理になります。
再帰的なアルゴリズムについては5章で説明します。
ノードの生成は,帰りがけ順になっています。
すなわち,次のように処理します。
ⅰ)データがなければ空ポインタを返す。
ⅱ)中央より左を左部分木として生成。
ⅲ)中央より右を右部分木として生成。
ⅳ)中央値のノードを生成し,
左部分木と右部分木にリンクをはる。
[プログラム処理]
private long 配列を木に変換(long Left,
long Right)
{
if(Right < Left) return -1;
long Center = (Left+Right)/2;
long PL = 配列を木に変換(Left,Center-1);
long PR = 配列を木に変換(Center+1,Right);
long P = getArea();
if(P < 0) { freeAll(PL); freeAll(PR);}
else
{
DataArea[P].Element.番号 =
tempData[Center].番号;
DataArea[P].Element.氏名 = tempData[Center].氏名;
DataArea[P].Element.点数 = tempData[Center].点数;
DataArea[P].Left=PL; DataArea[P].Right=PR;
}
return P;
}
(h)木の再構築
木を配列に移動して,開放した後,配列を木に変換します。
[プログラム処理]
private long 木の再構築(long P)
{
long N = count(P);
tempData = new ElementData[N];
木を配列に移動(P, 0);
freeAll(P);
long X = 配列を木に変換(0, N - 1);
tempData = new ElementData[0];
return X;
}
(i)番号探索
番号がLeft側にあるかRight側にあるかは
番号の大小比較で分かりますので,全件検索は必要ありません。
このため,効率のよい探索が可能です。
この処理も,再帰的な処理になります。
再帰的なアルゴリズムについては5章で説明します。
判定は,行きがけ順に行います。
ⅰ)ポインタが空なら見つからなかったものとする。
ⅱ)番号が等しければ,当該ノードを返却。
ⅲ)番号が小さければ,左部分木を探索。
ⅳ)番号が大きければ,右部分木を探索。
[プログラム処理]
private long 番号探索(long P,long 番号)
{
if(P < 0) return -1;
ElementData E = element(P);
if(番号 == E.番号) return P;
else if(番号 < E.番号) return 番号探索(left(P),番号);
else return 番号探索(right(P),番号);
}
(j)キーでないデータの探索
キーでないデータを探索するには,
そのデータがLeft側にあるかRight側にあるかが
分かりませんので,
全件探索を行う必要があります。
すなわち,
当該ノードであれば,探索終わり。
当該ノードでなければ,
左側を探索し,あれば探索終わり。
なければ右側を探索します。
この処理も,再帰的な処理になります。
再帰的なアルゴリズムについては5章で説明します。
判定は,行きがけ順に行います。
例として,氏名を探索する例を示します。
[プログラム処理]
private long 氏名探索(long P,string 氏名)
{
if(P < 0) return -1;
ElementData E = element(P);
if(string.Compare(氏名,E.氏名)
== 0)
return P;
long PL = 氏名探索(left(P),氏名);
if( PL >= 0) return PL;
return 氏名探索(right(P),氏名);
}
横型探索の場合,
訪問すべきノード番号を入れる表を用意し,
訪問したノードが探索対象でない場合,
そのノードのLeft,Rightのポインタを保管しておきます。
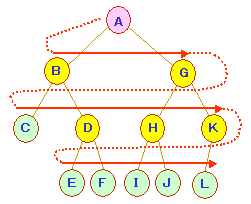
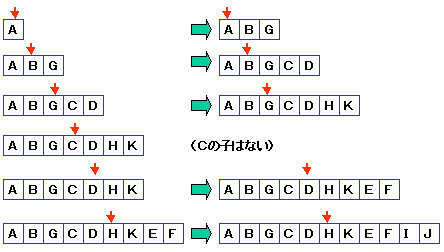
探索の手順は,以下のようになります。
(a) N=0,I = 0,訪問ノード表[N++]=ルートとする。
(b) I < Nの間,以下を繰り返す。
(b-1) 訪問ノード表[I]が探索すべきノードのとき検索終わり。
(b-2) leftが空でなければ,leftを訪問ノード表に追加。
(追加したとき,Nカウントアップ)
(b-3) rightが空でなければ,rightを訪問ノード表に追加。
(追加したとき,Nカウントアップ)
(b-4) Iをカウントアップ。
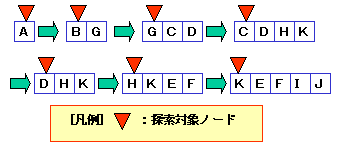
(訪問ノード表の動き)
private long 横型探索(long P,string 氏名)
{
long PP, PX; long Num=count(P);
long [] P_Array=new long[Num];
N=0:P_Array[N++]=P; int i=0;
while (i < N)
{
PP=P_Array[i];
ElementData E=element(PP);
if(string.Compare(氏名,E.氏名)
== 0) return PP;
PX=left(PP) ;if(PX>=0) P_Array[N++]=PX;
PX=right(PP);if(PX>=0)
P_Array[N++]=PX;
i++;
}
}
ところで,すでに探索したノードは保管する必要がありません。
領域がもったいないようであれば,待ち行列として実装します。
private void Enque(long V,ref int N, ref
long[] PA)
{ PA[N]=V; N++; }
private long Deque(ref int N,ref
long[]
PA)
{ long R=PA[0];N--; for(int k=0;k<N;k++)PA[k]=PA[k+1];
return R; }
private long 横型探索(long P,string
氏名)
{
long PP,PX;string S; long Num=count(P);
long [] P_Array=new long[Num];
int N=0;Enque(P,ref N,ref P_Array); int i=0;
while (N>0)
{
PP=Deque(ref N,ref P_Array);
ElementData E=element(PP);
if(string.Compare(氏名,E.氏名)
== 0) return PP;
PX=left(PP);if(PX>=0) Enque(PX,ref N,ref P_Array);
PX=right(PP);if(PX>=0) Enque(PX,ref N,ref P_Array);
}
return -1;
}
  
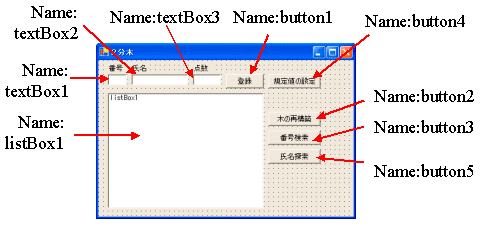
(7)例題
木構造の動きを確認するためのプログラム例を示します。
なお木の再構築では,理解しやすくするため,
途中経過の配列を表示するよう変更します。
その他の基本的な関数は(5),(6)に示しましたので
省略します。
private void 表示()
{
listBox1.Items.Clear(); 要素表示(DataP,"");
}
private void 未使用領域表示()
{
listBox1.Items.Clear(); long
P = ErasedP;
long PP;
while(P>=0)
{
PP=right(P);
listBox1.Items.Add(P.ToString() + "\t"
+ PP.ToString());
P=PP;
}
}
private void 要素表示(long P, String S)
{
if(P<0) return;
要素表示(DataArea[P].Left,
S + "
");
ElementData E = DataArea[P].Element;
listBox1.Items.Add(S+E.番号.ToString("0000")+"\t"+
E.氏名.ToString()+"\t"+E.点数.ToString());
要素表示(DataArea[P].Right,
S + "
");
}
private void Form1_Load(object
sender, System.EventArgs
e)
{
初期設定();DataP=-1; 表示();
}
private long 登録(long P,long 番号, string
氏名, int 点数)
{
if(P < 0)
{
long PP = getArea();if(PP < 0)
return -1;
DataArea[PP].Element.番号 = 番号;
DataArea[PP].Element.氏名 = 氏名;
DataArea[PP].Element.点数 = 点数;
DataArea[PP].Left = -1;
DataArea[PP].Right = -1;
return PP;
}
else if(番号 == DataArea[P].Element.番号)
{
DataArea[P].Element.氏名 = 氏名;
DataArea[P].Element.点数
= 点数;
}
else if(番号 < DataArea[P].Element.番号)
DataArea[P].Left = 登録(DataArea[P].Left
,番号,氏名,点数);
else DataArea[P].Right = 登録(DataArea[P].Right,番号,氏名,点数);
return P;
}
private void button1_Click(object sender,
System.EventArgs e)
{
try
{
DataP = 登録(DataP, long.Parse(textBox1.Text),
textBox2.Text,
int.Parse(textBox3.Text));
表示();
}
catch(Exception E)
{ MessageBox.Show(E.Message); }
}
private long 木の再構築(long P)
{
long N = count(P);
tempData = new ElementData[N]; 木を配列に移動(P,
0);
listBox1.Items.Clear();
for(int i = 0;i < N; i++)
{
ElementData E = tempData[i];
listBox1.Items.Add(E.番号.ToString()
+ "\t” +
E.氏名 +
"\t"+E.点数.ToString());
}
MessageBox.Show("一次元配列に変換しました");
freeAll(P);
long X = 配列を木に変換(0, N-1);
tempData = new ElementData[0];
return X;
}
private void button2_Click(object sender,
System.EventArgs e)
{
DataP = 木の再構築(DataP);
表示();
}
private string 先頭文字列(String
S)
{
string SS = S; string R = ""
int i = 0;
while(i < S.Length &&
S[i]
==' ') i++;
while(i < S.Length && S[i]
!=' ' && S[i]!='\t')
{ R = R + S[i].ToString(); i++;
}
return R;
}
private void listBox1_SelectedIndexChanged
(object
sender,
System.EventArgs e)
{
string S = 先頭文字列(listBox1.Text);
long N = long.Parse(S); long
P = 番号探索(DataP,N);
if(P >= 0)
{
ElementData E = element(P);
textBox1.Text = E.番号.ToString();
textBox2.Text = E.氏名;
textBox3.Text = E.点数.ToString();
}
}
private void button3_Click(object sender,
System.EventArgs e)
{
long P = 番号探索(DataP,long.Parse(textBox1.Text));
if(P < 0) MessageBox.Show("検索失敗");
else
{
ElementData E = element(P);
MessageBox.Show("\nP =” + P.ToString()+
"\nE =” + E.番号.ToString()+
"\n氏名=” +E.氏名+
"\n点数=” +E.点数.ToString()+
"\nLeft=” +left(P).ToString()+
"\nRight=”+right(P).ToString());
}
}
private void button4_Click(object sender,
System.EventArgs e)
{
DataP =登録(DataP,50, "山 田 孝 雄",
73);
DataP =登録(DataP,20, "三 枝 光 一",
64);
DataP =登録(DataP,30, "相 田 昌 枝",
50);
DataP =登録(DataP,80, "徳 田 修 二",
30);
DataP =登録(DataP,10, "白 江 幸太郎",
55);
DataP =登録(DataP,25, "山 本 和 久",
70);
DataP =登録(DataP,45, "相 馬 栄 三",
60);
DataP =登録(DataP,70, "原 口 健 一",
80);
DataP =登録(DataP,60, "幸 田 一 雄",
90);
DataP =登録(DataP,55, "君 田 美智代",
75);
表示();
}
private void button5_Click(object sender,
System.EventArgs e)
{
long P=氏名探索(DataP,textBox2.Text);
if(P<0) MessageBox.Show("検索失敗");
else
{
ElementData E=element(P);
MessageBox.Show("\nP ="+
P.ToString()+
"\nE ="+E.番号.ToString()+
"\n氏名="+E.氏名+
"\n点数="+E.点数.ToString()+
"\nLeft="+left(P).ToString()+
"\nRight="+right(P).ToString());
}
}
|
  
 1. 基本的なアルゴリズム 1. 基本的なアルゴリズム
 2. 基本的なデータ構造 2. 基本的なデータ構造
 3. 操作を伴うデータ構造 3. 操作を伴うデータ構造
 4. 探索 4. 探索
 5. 再帰的アルゴリズム 5. 再帰的アルゴリズム
 6. ソート 6. ソート
 7. 集合 7. 集合
 8. 文字列処理 8. 文字列処理
 9. 色々なアルゴリズム 9. 色々なアルゴリズム

上のタイトルをクリックします
|

 3.6 木構造
3.6 木構造