2．2 配列
番号 以下をクリックすると同位置にジャンプします （１） 配列の考え方 （２） 最大値を求める （３） 配列要素の逆転 （４） 素数を求める (a) 力任せ法 (b) 改良１ (c) 改良２ (d) 改良３（エラトステネスのふるい） （５） 文字列は文字型の配列 （１）配列の考え方 同じデータ型の集まりを配列（Array)と呼び， 次のように宣言します。 ■宣言方法 　　データ型[] 配列変数名 = new データ型[要素数]; ■データの代入： 　　配列変数名[インデックス] = データ; [例] 　　 Int[] A = new int[30]; 　　A[0]=70; A[1]=77; 　　　　　　図２−１　同じデータ型の集まり（配列） また，以下のように，要素数を宣言しないで， 値をまとめて代入することもできます。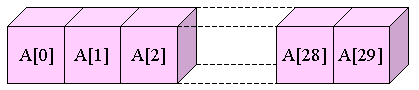 [形式１] 　　　 データ型[] 配列変数名; 　　　 配列変数名 = new データ型[]{データ，データ，…，データ} [例] 　　　 int[] A; A = new int[]{ 1, 2, 3, 4} [形式２] 　　　 データ型[] 配列変数名 = {データ，データ，…，データ} [例] string[] A = {“Zero”,”One”,”Two”,”Three”} ［Program 2−2］ 配列の初期値設定例　　　 private void Form1_Load(object sender, System.EventArgs e) { int i; 　int[] a=new int[]{20,26,11,32,68}; 　int na=a.Length; 　textBox1.Text = "要素数 : " + na.ToString() + "\r\n"; 　for (i = 0; i < na; i++) 　　　textBox1.Text += "\r\n a[" + i.ToString() + "] = " + 　　　　　　　　　　　　　 　a[i].ToString(); } ［Program 2−3］ 配列へのデータ設定例 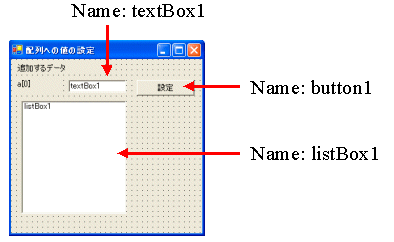　　　　　　　　　　　 　　　 //宣言分部 private int 配列数=0; private int[] 配列 =new int[11]; 　・ 　・ 　・ private void 配列の表示() { 　label2.Text="a[" + 配列数.ToString() + "]"； 　　listBox1.Items.Clear(); 　　for(int i=0; i<配列数; i++) 　　　　listBox1.Items.Add("a[" + i.ToString()+ "]=" +配列[i]); } private void button1_Click(object sender, System.EventArgs e) {　 try 　　{ 　if(配列数>10)MessageBox.Show("配列数が10を超えました"); 　　　　else 　　　　{ 　　　　　　配列[配列数]= int.Parse(textBox1.Text); 　　　　　　配列数 ++; 　　　　　　配列の表示(); 　　　　} 　　 } 　　 catch( Exception myError) 　　 { 　　　　MessageBox.Show(myError.Message); 　　 } } private void Form1_Load(object sender, System.EventArgs e) { 　　textBox1.Text=""; 　　listBox1.Items.Clear(); } 番号 以下をクリックすると同位置にジャンプします （１） 配列の考え方 （２） 最大値を求める （３） 配列要素の逆転 （４） 素数を求める (a) 力任せ法 (b) 改良１ (c) 改良２ (d) 改良３（エラトステネスのふるい） （５） 文字列は文字型の配列 （２）最大値を求める 　３値の最大値の延長で考えると，Program2-4が妥当に見えますが， これでは，個数が増えるたびに行数が増えてしまいます。 　そこで，値を入れ換える部分を次のように変えてみます。 　　i=1; if (MAX<a[i]) MAX = a[i]; 　　i=2; if (MAX<a[i]) MAX = a[i]; 　　i=3; if (MAX<a[i]) MAX = a[i]; 　　i=4; if (MAX<a[i]) MAX = a[i]; 　　i=5; if (MAX<a[i]) MAX = a[i]; i =1〜5 と変化させれば，if文の部分は共通になります。 ですから，次のように単純化できます。 　 for(int i=1; i<6;i++) if (MAX<a[i]) MAX = a[i]; さらに，配列のサイズはLengthプロパティを使って 　　　配列名.Length で取り出すことができますから， 　 for(int i=1; i<a.Length;i++) if (MAX<a[i]) MAX = a[i]; とすることで，要素数を気にしない表現ができます。 改善した例をProgram 2-5 に示します。 ［Program 2−4］ 最大値を求める単純な例　　 private int 最大値1(int[] a) {　int i; int MAX=a[0]; 　if (MAX<a[1]) MAX = a[1]; 　if (MAX<a[2]) MAX = a[2]; 　if (MAX<a[3]) MAX = a[3]; 　if (MAX<a[4]) MAX = a[4]; 　if (MAX<a[5]) MAX = a[5]; 　return MAX; } private void button1_Click(object sender, System.EventArgs e) {　 int[] a = new int[]{50,20,33,55,44,25}; 　　int b = 最大値1(a); 　　MessageBox.Show(b.ToString()); } ［Program 2−5］ 最大値を求める(改善例） private int 最大値1(int[] a) { int i; int MAX=a[0]; 　for(i=1; i<a.Length; i++) if (MAX<a[i]) MAX = a[i]; 　return MAX; } private void button1_Click(object sender, System.EventArgs e) {　 int[] a = new int[]{50,20,33,55,44,25}; 　　int b = 最大値1(a); 　　MessageBox.Show(b.ToString()); } 番号 以下をクリックすると同位置にジャンプします （１） 配列の考え方 （２） 最大値を求める （３） 配列要素の逆転 （４） 素数を求める (a) 力任せ法 (b) 改良１ (c) 改良２ (d) 改良３（エラトステネスのふるい） （５） 文字列は文字型の配列 （３）配列要素の逆転 配列要素の順序を逆転させるには，次のように， 最初と最後，２番目と最後からひとつ前， さらに３番目と最後から２つ前，・・・と交換していきます。 　　　　　　図２−２　配列要素の逆転 ２つの値を交換するには，通常，２つの要素以外の作業的な変数を用意して， 次のような手順で行います。 　　　　　　図２−３　データの交換方法 値を交換するような手続きを考える際，C#では注意が必要です。 旧来のCやC++では，標準的な引数の受け渡しは参照(Reffer)渡しですが C#での標準は，値（Value）渡しです。 これは，呼び出された側の代入等で， 呼び出し側の定数領域等が壊されることを避けるための処置のようです。 したがって，特に何も指定しなければ，呼び出された関数側で値を設定しても， 呼び出した側の値は変更されません。 呼び出した側の値を変更するような場合，呼び出す側，呼び出される側ともに 積極的に参照渡しであることを指定します。 [呼び出す側]　　　　swap( ref a[i], ref a[n-i-1]) [呼び出される側]　 private void swap( ref int X , ref int Y) { ・・・・・ } なお，プログラム例では，データ入力の手間を省くため， 逆転させる前のデータは乱数を発生させて設定しています。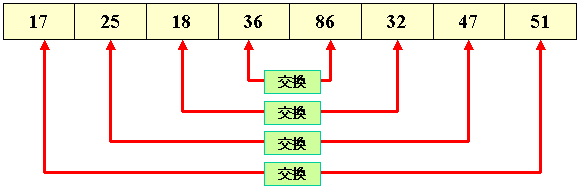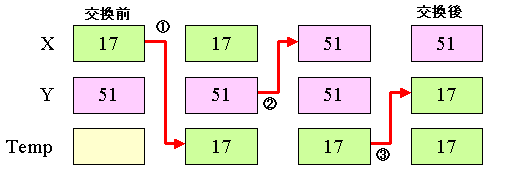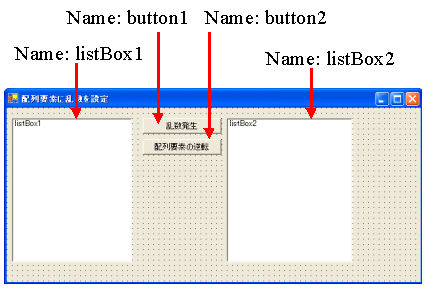 （button1_Click) ［Program 2−6］ 配列の逆転 　　　　　　 private int [] myArray = new int[10]; private void 配列の表示(ListBox A) { 　　A.Items.Clear(); 　　for(int i=0; i< myArray.Length; i++) 　　　　A.Items.Add("a[" + i.ToString()+ "]=" +myArray[i]); } private void button1_Click(object sender, System.EventArgs e) { 　　Random myRandom = new Random(); 　　for (int i=0; i<10;i++) myArray[i]=myRandom.Next(0,100); 　　配列の表示(listBox1); } private void swap( ref int X , ref int Y) { 　　int D = X; X = Y; Y = D; } private void 配列要素の逆転(ref int[] a) { 　　int n=a.Length; 　　for (int i = 0; i < n / 2; i++) swap( ref a[i], ref a[n-i-1]); } private void button2_Click(object sender, System.EventArgs e) { 　　配列要素の逆転(ref myArray); 　　　配列の表示(listBox2); } 番号 以下をクリックすると同位置にジャンプします （１） 配列の考え方 （２） 最大値を求める （３） 配列要素の逆転 （４） 素数を求める (a) 力任せ法 (b) 改良１ (c) 改良２ (d) 改良３（エラトステネスのふるい） （５） 文字列は文字型の配列 （４）素数を求める (a) 力まかせ法 素数の定義どおりに，その値より小さい値で割り切れないことを検査して， 素数かどうかを判定する方法です。 その様子を図２−４に示します。 図中の文字色は，次の意味を持っています。 　　赤：その数で除算したが割り切れなかった。 　　緑：その数で除算を行ったら割り切れた。 　　黒：その数での除算は不要なので行わない。 　　　 　　　　　　図２−４　力まかせ法による素数 ［Program 2−7］ 力まかせ法により素数を求める。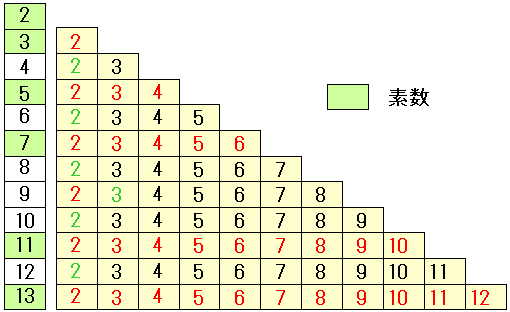 　　　　　　 private long 素数計算1() //力まかせ法 {　 int i,n; long 計算数 =0; 素数の数=0; 　　for(n = 2; n <=1000; n++) 　　{ 　　　　for (i = 2; i<n; i++) 　　　　 {　計算数++; // 計算回数のカウント 　　　　　　if ((n % i) == 0) break; // 余りが0であれば割り切れた 　　　　 } 　　　　 if (n == i)素数[素数の数++] = n; // 最後まで割り切れなければ 　　 }　　　　　　　　　　　　　　　　　　　　　　// 素数とみなす 　　return 計算数; } private void 表示(Label label, ListBox list,long X) {　 int i; 　　label.Text="割り算回数=" + X.ToString("#,##0"); 　　list.Items.Clear(); 　　for(i=0; i<素数の数; i++) list.Items.Add(素数[i].ToString("#,##0")); } private void button1_Click(object sender, System.EventArgs e) { 　　表示(label1, listBox1,素数計算1()); } 番号 以下をクリックすると同位置にジャンプします （１） 配列の考え方 （２） 最大値を求める （３） 配列要素の逆転 （４） 素数を求める (a) 力任せ法 (b) 改良１ (c) 改良２ (d) 改良３（エラトステネスのふるい） （５） 文字列は文字型の配列 (b) 改良１ ２や３で割り切れなければ，４（＝２×２）や６（＝２×３）でも 割り切れません。 しかし，力まかせ法では，４や６でも割り切れるかどうかを判定しています。 これは，無駄ですので，求まった素数を配列に格納しておき， 既に求まった素数で割り切れるかどうかを判定すれば構いません。 　　　　　 　　　　　　図２−５　素数計算（改良１） ［Program 2−8］ 素数計算(改良１）：表示は力まかせ法と同じ 　　　　　　 private long 素数計算2() //改良1 { 　　int i,n; long 計算数 =0; //計算回数 　　素数の数=0; 素数[素数の数++] = 2; 素数[素数の数++] = 3; 　　for(n = 5; n <=1000; n += 2) 　　 { 　　　　　for (i = 1; i<素数の数; i++) 　　　　　{ 　　　　　　　計算数++; // 計算回数のカウント 　　　　　　　if ((n % 素数[i]) == 0) break; // 余りが0であれば割り切れた 　　　　　} 　　　　　if (素数の数 == i)素数[素数の数++] = n; // 最後まで割り切れなければ 　　　} 　　　　　　　　　　　　　　　　　　　　　　　　　　 　// 素数とみなす 　　　return 計算数; } private void button2_Click(object sender, System.EventArgs e) { 　　表示(label2, listBox1,素数計算2()); } 番号 以下をクリックすると同位置にジャンプします （１） 配列の考え方 （２） 最大値を求める （３） 配列要素の逆転 （４） 素数を求める (a) 力任せ法 (b) 改良１ (c) 改良２ (d) 改良３（エラトステネスのふるい） （５） 文字列は文字型の配列 (c) 改良２ 今，１００の約数を考えてみると，次のように 割り切れる数のすべてが，最初の４通りに入っています。 すなわち，最初の４通りで割り切れなければ， 素数として判別してもよいことになります。 　２×５０ 　 割り切れる数の すべてが この範囲内に入る。 Ｎの平方根以下の素数で 割り切れなければ， 素数として判別してよい。 　４×２５ 　５×２０ １０×１０ ２０×　５ ２５×　４ ５０×　２ これらの関係を図２−６に示すと，乗数と非乗数の組合せは， 対称になっていることが分かります。 すなわち，Ｎの平方根以下の素数で割り切れなければ， 素数とみなしてよいことが分かります。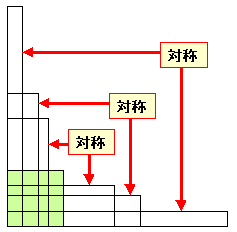 　　　　　　　　 　　　　　　　　　　図２−６　約数はお互いに対称 ［Program 2−9］ 素数計算(改良2）：表示は力まかせ法と同じ 　　　　　　 private long 素数計算3() //改良2 { 　　int i,n;　long 計算数 =0; //計算回数 　　素数の数=0; 素数[素数の数++] = 2; 素数[素数の数++] = 3; 　　for(n = 5; n <=1000; n += 2) 　　{ 　　　　　bool flag = true; 　　　　　for (i = 1; 素数[i]*素数[i] <=n; i++) 　　　　　{ 　　　　　　　計算数++; // 計算回数のカウント 　　　　　　　if ((n % 素数[i]) == 0) 　　　　　　　　　　　　 { flag=false; break; } // 余りが0であれば割り切れた 　　　　　} 　　　　　if (flag) 素数[素数の数++] = n; // 最後まで割り切れなければ 　　 }　　　　　　　　　　　　　　　　　　　　　　 // 素数とみなす 　　return 計算数; } private void button3_Click(object sender, System.EventArgs e) { 　　表示(label3, listBox1,素数計算3()); } 番号 以下をクリックすると同位置にジャンプします （１） 配列の考え方 （２） 最大値を求める （３） 配列要素の逆転 （４） 素数を求める (a) 力任せ法 (b) 改良１ (c) 改良２ (d) 改良３（エラトステネスのふるい） （５） 文字列は文字型の配列 (d) 改良３（エラトステネスのふるい） 十分なメモリ量があれば，Ｎ以下の整数をすべて書き並べておいて， 素数の倍数を消していくことで，素数を求める方法です。 この方法は，一切除算を使いませんので，効率のよい方法です。 提唱者の名前から エラトステネスのふるい(sieve of Eratosthenes）と呼ばれます。 手順は以下のとおりです。 （１）２以上Ｎ以下の整数をすべて書き並べておく。 （２）２の倍数をすべて消す。 （３）残った最小の数（最初は３）の倍数をすべて消す。 （４）３を繰り返す。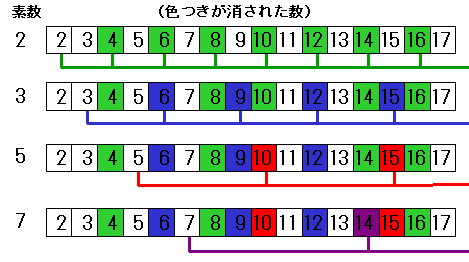 　　　　　　　　　　図２−６　約数はお互いに対称 ［Program 2−10］ エラトステネスのふるい（改良3）：表示は力まかせ法と同じ 　　　　　　 private long 素数計算4() //エラトステネスのふるい(sieve of Eratosthenes) { 　　int i,j; 　　for(i=2; i<=1000;i++) ふるい[i]=i; 　　for(i=2; i<=1000;i++) 　　　if(ふるい[i] != 0) for( j = 2*i; j<=1000; j+=i) ふるい[j]=0; 　　素数の数=0; 　　for(i=2; i<=1000;i++)if(ふるい[i] !=0) 素数[素数の数++]=ふるい[i]; 　　return 0; } private void button4_Click(object sender, System.EventArgs e) { 　　表示(label4, listBox1,素数計算4()); } 番号 以下をクリックすると同位置にジャンプします （１） 配列の考え方 （２） 最大値を求める （３） 配列要素の逆転 （４） 素数を求める (a) 力任せ法 (b) 改良１ (c) 改良２ (d) 改良３（エラトステネスのふるい） （５） 文字列は文字型の配列 （５）文字列は文字型の配列 文字列は，文字の配列として表現されています。 [Program 2-11]は，ツェラーの公式で得られた曜日の番号によって 曜日を表示するプログラムです。 　番号　 0 1 2 3 4 5 6 　曜日 　日　 　月　 　火　 　水　 　木　 　金　 　土　 まず，曜日の文字列を string で指定しておき， 曜日の番号をインデックスとして文字型のデータを取り出しています。 ［Program 2−11］ 文字列を文字型の配列として使う。 　　　　　 // ツェラー(Zeller)の公式 private int WeekDay(int Y, int M, int D) { 　　　int YY=Y; int MM=M; 　　　if (M<3){YY=Y-1; MM=M+12;} 　　　return (YY +(YY/4)-(YY/100)+(YY/400)+(13*MM + 8)/5+D) % 7; } private void button1_Click(object sender, System.EventArgs e) { 　　int Y=int.Parse(textBox1.Text); 　　int M=int.Parse(textBox2.Text); 　　int D=int.Parse(textBox3.Text); 　　int R=WeekDay(Y,M,D); 　　string X="日月火水木金土"; 　　label4.Text = X[R]+"曜日" } 番号 以下をクリックすると同位置にジャンプします （１） 配列の考え方 （２） 最大値を求める （３） 配列要素の逆転 （４） 素数を求める (a) 力任せ法 (b) 改良１ (c) 改良２ (d) 改良３（エラトステネスのふるい） （５） 文字列は文字型の配列 1. 基本的なアルゴリズム 2. 基本的なデータ構造 3. 操作を伴うデータ構造 4. 探索 5. 再帰的アルゴリズム 6. ソート 7. 集合 8. 文字列処理 9. 色々なアルゴリズム 上のタイトルをクリックします