   
（１）クイックソートとは
クイックソート（Quick sort）とは，
グループ分けの基準とする要素（枢軸：pivotと呼ぶ）より
小さいグループと大きいグループに分割する作業を
繰り返すことによってソートする方法です。
クイックソートという呼称は，他のソートに比べ高速であるため，
考案者のC.A.Hoareによって名付けられものです。
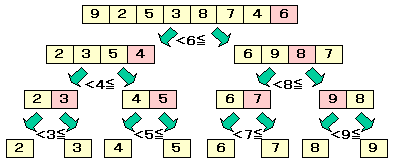
（２）分割の手順
まず，配列両端のポインタ Left，Rightを用意し，
以下の操作を行う。
@）A(Left)≧枢軸となる要素まで右方向にスキャンする。
A）A(Right)≦枢軸となる要素まで左方向にスキャンする。
B）A(Left)とA(Right)を交換する。
これを繰り返すことで，枢軸より小さい要素が左側に，
枢軸と等しいか大きい要素が右側に集まります。
以下の例は，６を枢軸とした場合の例です
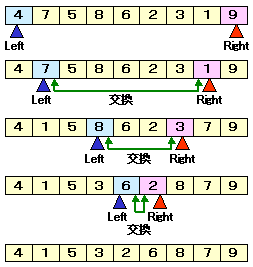
以下は，枢軸を配列の中央の値としたときの
分割のプログラム例です。
int pleft = 0;
int pright = n - 1;
int x = a[(pleft + pright) / 2];
do
{
while(a[pleft] < x) pleft++;
while(a[pright] > x) pright--;
if (pleft <= pright)
{
swap(ref a[pleft], ref a[pright]);
pleft++; pright--;
}
} while (pleft <= pright);
|
// 左カーソル
// 右カーソル
// 配列の中央を枢軸とする
// 左カーソルの走査
// 右カーソルの走査
// 交換
|
（３）枢軸の選択
最も簡単な方法は，配列の左端，中央，右端のいずれかを
枢軸として採用することです。
しかし，次の例で９を選ぶと，
ただ１つの要素とその他の要素列に分解されてしまいます。
クイックソートの時間計算量は，理想的にはＯ(N
log N)ですが，
ただひとつの要素と，それ以外の要素という分割が続くと
n回の分割が必要となり，最悪時間計算量はＯ(N
2)となってしまいます。
理想的には，全要素の中央値を枢軸として選ぶと良いのですが，
中央値選択の時間がかかってしまいます。
ソートのスピードアップが目的ですから，
中央値を求めるのに時間がかかってしまっては，本末転倒です。
そこで，
左端，中央，右端の３値の中央値を求めることで，
最悪の選択を避ける方法が一般的です。
このための処理は，以下のような簡単な手続きで実現できます。
int x = a[(pleft + pright) / 2];
int x1 = a[pleft];
int x2 = a[pright];
if((x <= x1 && x1 <=
x2)||(x2
<= x1 && x1 <= x)) x
= x1;
if((x <= x2 && x2 <=
x1)||(x1
<= x2 && x2 <= x)) x
= x2;
（４）ソートの処理
ソートは，以下の手順で行われます。
@）枢軸の選択
A）配列を分割
B）左右を更に再分割（ただし，要素数が１のときは行わない）
以下のように，
配列を分割した直後のポインタで左右を再分割するかどうかを決めます。
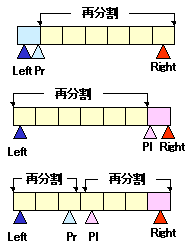
［プログラム］
private void Quick(ref int [] a,int left,
int right)
{
int pleft =left;
int pright =right;
int x = a[(pleft + pright) / 2];
// 枢軸の選択
int x1 = a[pleft];int x2 =
a[pright];
if((x <= x1 && x1 <=
x2)||(x2 <= x1 && x1 <= x))
x=x1;
if((x <= x2 && x2
<=
x1)||(x1 <= x2 && x2 <=
x))
x=x2;
do
{
while(a[pleft] < x) pleft++;
// 枢軸以上の走査
while(a[pright] > x) pright--; //
枢軸以下の走査
if (pleft <= pright)
{
swap(ref a[pleft], ref a[pright]); //
枢軸以上，以下の交換
pleft++; pright--;
}
} while (pleft <= pright);
if(left < pright) Quick(ref a,
left, pright);
if(pleft < right ) Quick(ref a,
pleft, right);
}
private void クイックソート()
{
Quick(ref Data, 0, Data.Length-1);
}
（５）非再帰クイックソート
再帰的アルゴリズムの章で説明したように，
再帰的な処理はスタックを用いて非再帰的な手続きに変換できます。
クイックソートにおける分割の様子をみてみましょう。
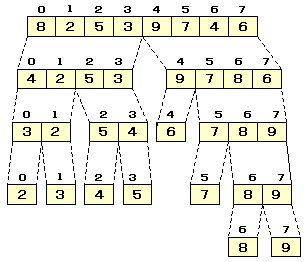
ある分割を行っている際，未だ分割していない範囲を
保存しておく必要があります。これをスタックにとります。
スタックの動きは，以下のようになります。
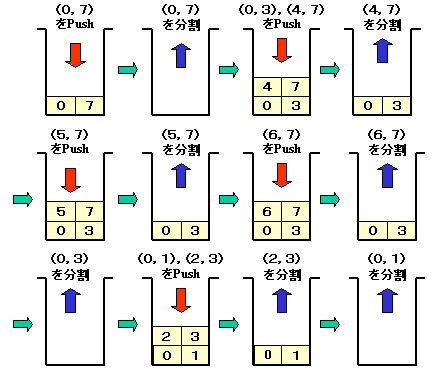
のソートは，以下の手順で行われます。
［プログラム］
private void 非再帰クイックソート()
{
int left, right; int ptr = 0;
int[] leftStack =new int[10];
int[] rightStack=new int[10];
leftStack[0] = 0;
rightStack[0] = Data.Length-1;
ptr++;
while (ptr-- > 0)
{
int pleft =left = leftStack[ptr];
int pright=right = rightStack[ptr];
int x = Data[(pleft + pright)
/ 2];
int x1 = Data[pleft];
int x2 = Data[pright];
if((x <= x1 && x1
<= x2)||(x2 <= x1 && x1 <=
x)) x=x1;
if((x <= x2 && x2
<= x1)||(x1 <= x2 && x2 <=
x)) x=x2;
do
{
while(Data[pleft] < x)
pleft++;
while(Data[pright]
> x)
pright--;
if (pleft <= pright)
{
swap(ref Data[pleft],
ref Data[pright]);
pleft++; pright--;
}
} while (pleft <= pright);
if(left < pright)
{
leftStack[ptr] = left; rightStack[ptr]
= pright;
ptr++;
}
if(pleft < right )
{
leftStack[ptr] = pleft; rightStack[ptr]
= right;
ptr++;
}
}
}
（６）非再帰クイックソートのスタックサイズ
前の例では，先頭側の分割，末尾側の分割の順に行っていますが，
どちら側を先に分割しても結果は同じになるはずです。
すなわち，
if(left < pright)
{
leftStack[ptr] = left; rightStack[ptr]
= pright;
ptr++;
}
if(pleft < right )
{
leftStack[ptr] = pleft;
rightStack[ptr]
= right;
ptr++;
}
としても，
if(pleft < right )
{
leftStack[ptr] = pleft;
rightStack[ptr]
= right;
ptr++;
}
if(left < pright)
{
leftStack[ptr] = left; rightStack[ptr]
= pright;
ptr++;
}
としても結果は変わりません。
さて，ここで，
要素数が多い方を先に分割（要素数が少ない方を先にＰｕｓｈ）する方法と
要素数が少ないほうを先に分割（要素数が多い方を先にＰｕｓｈ）する方法を
比較してみましょう。
スタックの動きをみるために，次のような分割を例にとります。
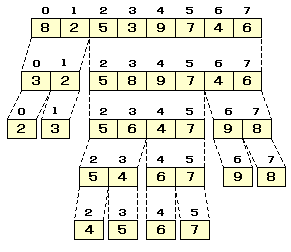
要素数が少ないほうを先にプッシュすると，
スタックの状態は以下のようになります。
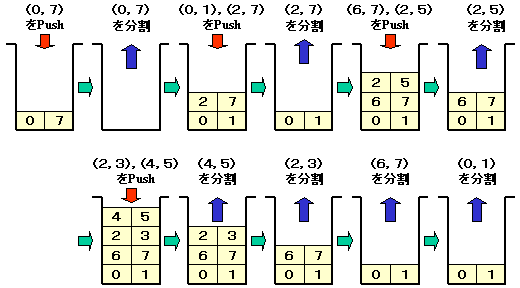
逆に，要素数が多いほうを先にプッシュすると，
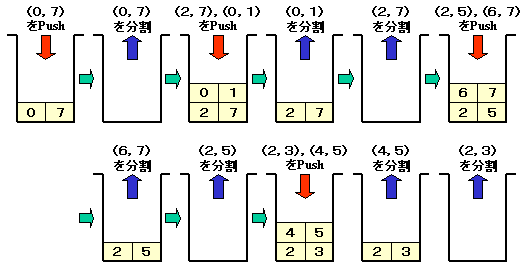
となり，Push／Popの回数は変わりませんが，
スタックの深さは浅くなります。
これは，一般に，配列の要素数が少ないほど，
少ない回数で分割が終了することに起因します。
ですから，
小さいほうの分割を先にやる（小さいほうを後からＰｕｓｈ）ほうが，
スタックサイズが小さくて済みます。
このようにすることによって，データ数がNのとき，
スタックの深さをlog Nで収めることができます。
例えば，要素数＝1,000,000のとき，
スタックの深さ＝20で済むことになります。
［演習］
例題のプログラムを変更して，要素数が少ないほうを優先的に分割する
（要素数が多いほうを先にPushする）よう書き換えてみて下さい。
 1. 基本的なアルゴリズム
2. 基本的なデータ構造
3. 操作を伴うデータ構造
4. 探索
5. 再帰的アルゴリズム
6. ソート
7. 集合
8. 文字列処理
9. 色々なアルゴリズム
上のタイトルをクリックします
|
6．6 クイックソート