   
（１）シェルソートとは
単純挿入法によるソートは，単純交換法，単純選択法と同様，
計算量はＯ（Ｎ2）です。
一方，単純挿入法には，以下の特徴があります。
(a) ソート済み，またはそれに近いとき高速である。
(b) 挿入先が離れているとき，ずらす回数が多くなる。
最初，なるべく離れた要素をグループ化して，
大まかなソートを行い，そのグループを縮めていくことで，
(a)の長所を活かし，（b)の短所を補うことができます。
この方法をシェルソートと呼びます。
まず，以下の例を単純挿入法でソートすると，
要素をずらす回数は，14回になります。
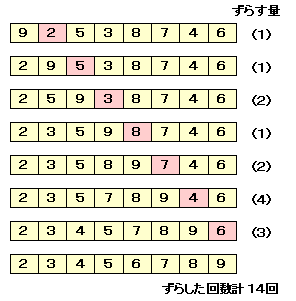
ここで，まず4つずつ離れたグループ
｛９，８｝，｛２，７｝，｛５，４｝，｛３，７｝
でソートすることを考えます。すると，次のようになります。
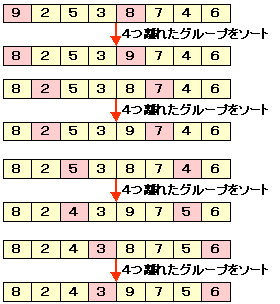
このソートを４−ソートと呼びます。
次に2つずつ離れたグループ
｛８，４，９，５｝，｛２，３，７，６｝
内でソート（２−ソート）します。
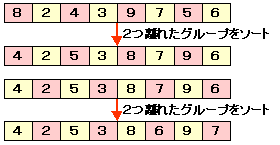
最後に，通常の単純挿入法でソートしてみます。
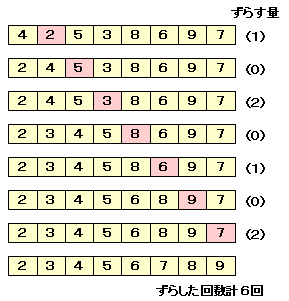
ずらす回数は，最初の単純な14回から6回に減っています。
［プログラム例］
private void シェルソート()
{
int i,j,h, Tmp;
for(h = Data.Length / 2 ; h
> 0;
h /= 2)
for(i = h; i < Data.Length;
i++)
{
Tmp=Data[i];
for(j = i - h ; j >=
0 && Data[j] > Tmp; j -= h)
Data[j + h]=Data[j];
Data[j + h]=Tmp;
}
}
（２）増分の選択
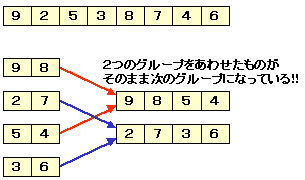
前の例では，等増分を４，２，１と変化させましたが，
以下のように，４−ソートの２グループをあわせたものが，
２−ソートのグループになってしまっています。
しかし，各段階のソートでなるべくかき混ぜるほうが，
各段階のソート結果を反映することになりますので，
効率よくなるはずです。
このためには，増分がお互いの倍数にならないようにします。
たとえば，次のようにします。
増分=1, 4, 13, 40, 121 （１から始めて3倍して１を加える）
ただし，増分が大きすぎても効果がないことが知られていますから，
最大増分量は，配列の要素数／９を超えないようにします。
このようにして改良した方法が，以下のプログラム例です。
［プログラム例］
private void シェルソート改良版()
{
int i, j, h, Tmp;
for(h = 1; h < Data.Length / 9;
h = h * 3 + 1);
for( ; h>0; h /= 3)
for(i = h; i < Data.Length;
i++)
{
Tmp = Data[i];
for(j = i - h ; j >= 0
&& Data[j] > Tmp; j -= h)
Data[j + h] = Data[j];
Data[j + h]=Tmp;
}
}
 1. 基本的なアルゴリズム
2. 基本的なデータ構造
3. 操作を伴うデータ構造
4. 探索
5. 再帰的アルゴリズム
6. ソート
7. 集合
8. 文字列処理
9. 色々なアルゴリズム
上のタイトルをクリックします
|
6．5 シェルソート