  
(1)文字列探索とは
文字列探索(string searching)とは,
ある文字列の中に,別の文字列が含まれているかどうか,
含まれている場合は,その位置を示すことです。
探索される側の文字列をテキスト(text),
探し出すための文字列をパターン(pattern)といいます。
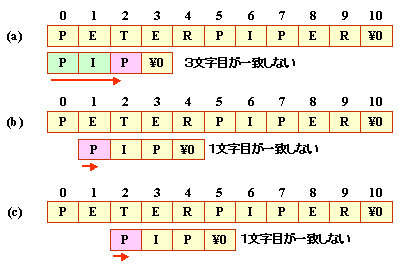
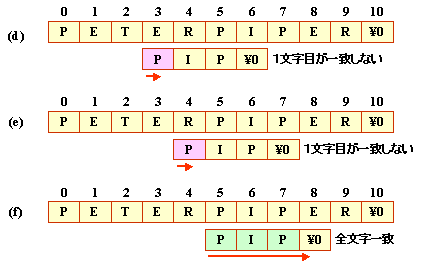
(2)力まかせ法
パターンを1文字ずつずらしながら,
テキスト中の文字列と照合していく単純な方法を
力まかせ法(brute forth method),単純法,素朴法等と呼びます。
[プログラム例]
private int 力まかせ法(string 文字列,
string パターン)
{
int P1=0; int P2=0;
while(P1<文字列.Length &&
P2<パターン.Length)
{
if(文字列[P1] == パターン[P2]){
P1++; P2++;}
else { P1 = P1 - P2 +
1; P2
= 0; }
}
if(P2==パターン.Length) return(P1
- P2);
return -1;
}
private void button2_Click(object
sender,
System.EventArgs e)
{
string 文字列 = textBox1.Text;
string パターン = textBox2.Text;
label5.Text=力まかせ法(文字列,
パターン).ToString();
}
  
(3)KMP法
力まかせ法では,不一致文字があると,
パターンを移動して再びパターンの先頭から照合しています。
すなわち,それまでの照合結果が捨てられることになります。
そこで,
D. E. KnuthとV. R. Pratt,J. H. Morris が,ほぼ同時期に考案した
Knuth-Pratt-Morris 法,略してKMP法と呼ばれる方法では,
パターンの文字列の特徴を活かして
そこまでの照合結果を有効活用して探索します。
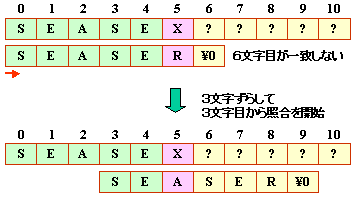
たとえば,以下のような探索を考えてみましょう。
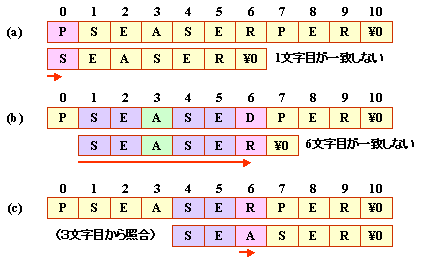
(b)の段階では,6文字目が一致しませんが,
パターンの1,2文字目と4,5文字目が同じですから,
3文字目から照合を始めれば良いことになります。
このようにパターンの特徴を活かすことで,
照合する開始位置を省略することができます。
ただし,照合のたびに照合開始位置を決めるのは効率が悪いので,
最初にテーブルを作成します。
(a) 1文字目で不一致の場合
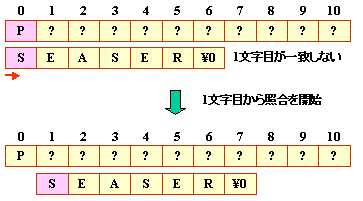
(b) 2文字目で不一致の場合
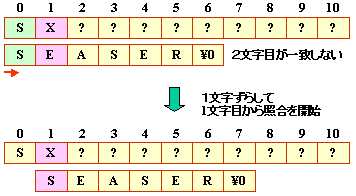
(c) 3文字目で不一致の場合
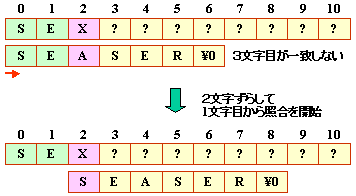
(d) 4字目で不一致の場合
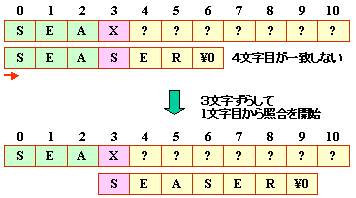
(e) 5字目で不一致の場合
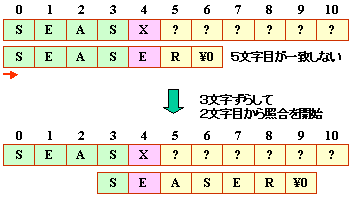
(f) 6字目で不一致の場合
■照合再開位置の設定
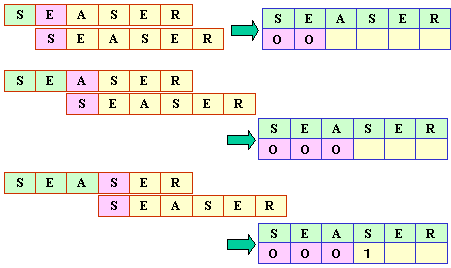
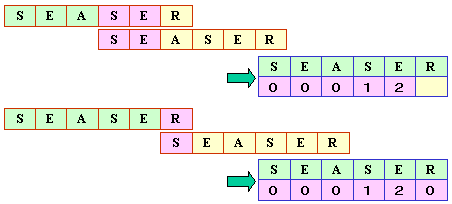
テーブルを作成するためには,パターン同士を1文字ずつずらしなら
以下のように,連続的に一致する文字数を
カウンすることで作成することができます。
[プログラム例]
private int KMP法(string 文字列, string
パターン)
{
int P1=1; int P2=0; int[] skip=new
int[256];
skip[P1]=0;
while (P1<パターン.Length)
{
if(パターン[P1]==パターン[P2])
skip[++P1]=++P2;
else if(P2==0) skip[++P1]=P2;
else P2=skip[P2];
}
P1=P2=0;
while(P1<文字列.Length &&
P2<パターン.Length)
{
if(文字列[P1] == パターン[P2]){
P1++; P2++;}
else if(P2 == 0) P1++;
else P2=skip[P2];
}
if(P2==パターン.Length) return(P1
- P2);
return -1;
}
private void button3_Click(object sender,
System.EventArgs e)
{
string 文字列 = textBox1.Text;
string パターン = textBox2.Text;
label5.Text=KMP法(文字列, パターン).ToString();
}
  
(4)BM法
この方法は,
R. S. BoyerとJ. S. Moore により提案したアルゴリズムで,
KMP法より簡単なアルゴリズムですが,効率のよい方法です。
Boyer-Moore 法,略してBM法と呼ばれます。
照合をパターンの末尾から行います。
一致しない文字を見つけた場合,
事前に用意した表により移動量を決めます。
例えば,以下のように4文字目で不一致のとき,
3文字ずらしても不一致になります。
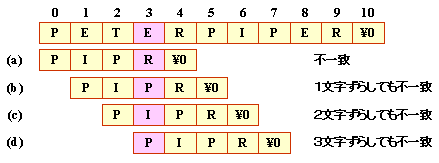
これは,テキストの4文字目の”E”という文字が,
パターンに入っていないからです。
すなわち,パターンに入っていない文字を見つけたら,
文字数分をずらすことができます。
以下のように一致した場合は,ひとつ前の文字で比較します。
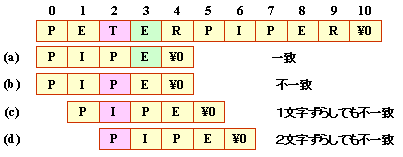
このとき2文字ずらしても不一致ですので,
3文字分ずらしてよいことになります。
以下のように,パターンの文字数分が一致すれば,成功です。
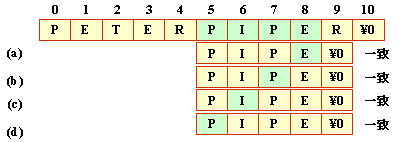
最初,以下のようなスキップ表を作成しておきます。
ここで,パターンの文字数をN,
パターンの最後に出現する位置の添え字をKとします。
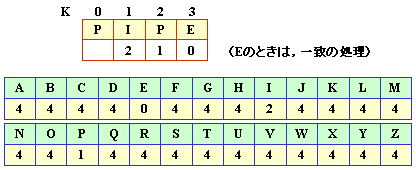 テーブル テーブル
[プログラム例]
private int BM法(string 文字列, string
パターン)
{
int P1=0; int P2=0;
int txtLen = 文字列.Length;
int patLen = パターン.Length;
int[] skip=new int[char.MaxValue+1];
for(P1 =0; P1 <= char.MaxValue;
P1++) skip[P1]=patLen;
for(P1 =0; P1 <= patLen
- 1;P1++)
skip[パターン[P1]]=patLen - P1 -1;
// このとき,P1= patLen-1であることに注意
while(P1<文字列.Length)
{
P2=patLen - 1;
while(文字列[P1] == パターン[P2])
{
if (P2==0) return(P1);
P1--; P2--;
}
P1 += skip[文字列[P1]];
}
return -1;
}
private void button4_Click(object sender,
System.EventArgs e)
{
string 文字列 = textBox1.Text;
string パターン = textBox2.Text;
label5.Text=BM法(文字列, パターン).ToString();
}
  
 1. 基本的なアルゴリズム 1. 基本的なアルゴリズム
 2. 基本的なデータ構造 2. 基本的なデータ構造
 3. 操作を伴うデータ構造 3. 操作を伴うデータ構造
 4. 探索 4. 探索
 5. 再帰的アルゴリズム 5. 再帰的アルゴリズム
 6. ソート 6. ソート
 7. 集合 7. 集合
 8. 文字列処理 8. 文字列処理
 9. 色々なアルゴリズム 9. 色々なアルゴリズム

上のタイトルをクリックします
|

 8.3 文字列探索
8.3 文字列探索













 テーブル
テーブル