  
（１）集合と要素
ものの集まりを集合（set）といいます。
集合中の個々のものを要素（element）といいます。
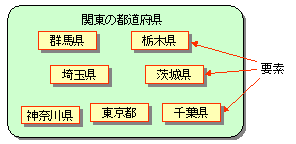
たとえば，以下は，関東の都道府県の集合です。
（２）集合の式表現
集合Xが要素2,6を持つとき，以下のように記述します。
X = {2, 6}
順序は意味を持ちませんので，
X = ｛6, 2}
は同じことを示します。
■元として含まれる
要素 a が集合Xの要素のとき，a はXに属するといい，
a ∈ X または X∋ a （元として含まれる）
と記述します。
要素 b が集合Xの要素でないとき，
b  X または X b （元として含まれる）
と記述します。
集合中の個々のものを要素（element）といいます。
たとえば，以下は，関東の都道府県の集合です。
■集合の要素数
要素数が無限大のとき無限集合，要素数の有限のとき有限集合と呼び，
|X| = ∞ ，|X| = n
等と記述します。
ただし，|X| = 0 のとき，空集合と呼び，φで表します。
■部分集合
集合Aのすべての要素が集合Bの要素であれば，
「AはBに含まれる」といい，
「AはBの部分集合（subset）である」といいます。
この関係は，次のように記述します。
A⊆B
Aの要素とBの要素がすべて等しい場合は，
A⊆B かつ B⊆A
であり， A≡B と記述します。
なお A⊆B かつ A≠B のとき，
AはBの真部分集合（proper subset）であるといい，
A⊂B
と記述します。
（３）集合の演算
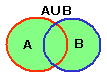
■和集合
集合A，Ｂの少なくとも一方に属している要素の集合を
和集合といいます。
たとえば，Ａ＝｛1, 2, 3, 5｝, Ｂ＝｛1, 3,
6, 7｝のとき，
Ａ∪Ｂ＝｛1, 2, 3, 5, 6,
7｝
となります。
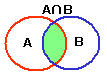
■積集合
集合A，Ｂの両方に属している要素の集合を
積集合といいます。
たとえば，Ａ＝｛1, 2, 3, 5｝, Ｂ＝｛1,
3,
6, 7｝のとき，
Ａ∩Ｂ＝｛1, 3｝
となります。
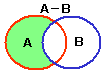
■差集合
集合Aの要素であって，集合Ｂの要素でない要素の集合を
差集合といいます。
たとえば，Ａ＝｛1, 2, 3, 5｝, Ｂ＝｛1,
3,
6, 7｝のとき，
Ａ−Ｂ＝｛2, 5｝
となります。
 1. 基本的なアルゴリズム
2. 基本的なデータ構造
3. 操作を伴うデータ構造
4. 探索
5. 再帰的アルゴリズム
6. ソート
7. 集合
8. 文字列処理
9. 色々なアルゴリズム
上のタイトルをクリックします
|
7．1 集合とは