   
乮侾乯僸乕僾
僸乕僾乮heap乯偲偼丆乽椵愊乿丆乽愊傒廳側偭偨傕偺乿
偲偄偆堄枴偱偡偑丆
偙偙偱偼丆恊偺抣偑巕嫙偺抣埲忋偱偁傞傛偆側姰慡俀暘栘傪
堄枴偟傑偡丅
偨偲偊偽丆師偺傛偆側栘傪僸乕僾偲偄偄傑偡丅
丂丂丂丂丂丂丂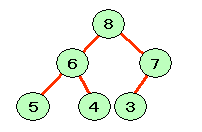
偨偩偟丆俀暘扵嶕栘偲堎側傝丆
昁偢偟傕嵍偺僲乕僪偑塃偺僲乕僪傛傝彫偝偄偲偼尷傝傑偣傫丅
乮俀乯姰慡俀暘栘偺攝楍偵傛傞昞尰
姰慡俀暘栘傪師偺傛偆偵攝楍偱昞尰偟傑偡丅
仭儖乕僩傪俙乵0乶偵擖傟傞丅
仭偦偺捈愙偺嵍偺巕傪俙乵侾乶偵丆塃偺巕傪俙乵俀乶偵擖傟傞丅
仭峏偵侾偮壓棳偵壓偭偰嵍偐傜奿擺偡傞
丂丂丂丂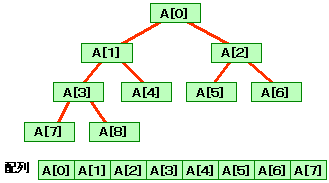
偙偺傛偆偵攝抲偡傞偲丆恊巕偺埵抲娭學偼丆師偺傛偆偵側傝傑偡丅
仭俙乵俬乶偺恊偼丆俙乵乮俬亅侾乯乛俀乶
仭俙乵俬乶偺嵍偺巕偼丆俙乵俬仏俀亄侾乶
仭俙乵俬乶偺塃偺巕偼丆俙乵俬仏俀亄俀乶
椺偊偽丆師偺傛偆偵攝抲偟傑偡丅
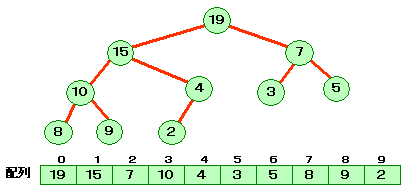
乮俁乯僸乕僾僜乕僩
僸乕僾傪棙梡偡傞偙偲偱丆埲壓偺庤弴偱僜乕僩偡傞偙偲偑偱偒傑偡丅
丂鶣乯僸乕僾偺儖乕僩偐傜抣傪庢傝弌偡偲嵟戝抣偑摼傜傟傞丅
丂鶤乯僸乕僾偺嵟屻偺梫慺傪愭摢偵堏偟丆僸乕僾傪嵞峔抸偡傞丅
丂鶥乯嵟戝抣傪攝楍偺嵟屻偵擖傟傞丅
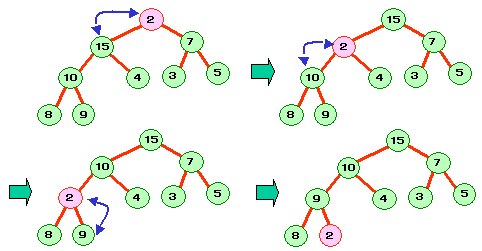
僸乕僾偺嵞峔抸偼師偺傛偆偵峴偄傑偡丅
丂鶣乯崻傪庢傝弌偟丆偦偙偵僸乕僾嵟屻偺梫慺傪堏摦
丅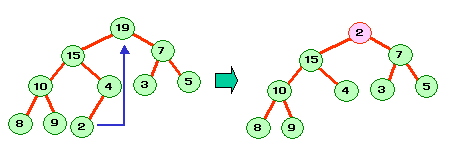
丂鶤乯 俀偮偺巕傪斾妑偟丆戝偒偄曽偺巕偲岎姺偡傞丒
丂鶥乯 儕乕僼偵撏偔,傑偨偼嵍塃偺巕偑帺暘傛傝彫偝偔側傞傑偱
丂丂丂 鶤乯傪孞傝曉偡丅
乮係乯僸乕僾偺峔抸
僸乕僾傪峔抸偡傞偵偼丆壓棳懁偺晹暘栘偐傜儃僩儉傾僢僾揑偵愊傒忋偘傑偡丅
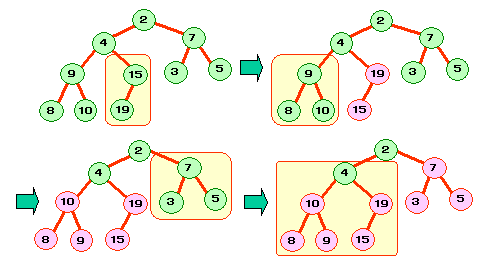
嵟屻偺張棟偼丆僸乕僾偺嵞峔抸偺張棟偲傎傏摨偠偵側傝傑偡丅
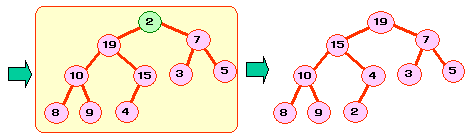
偙偺堄枴偱丆僸乕僾慡懱偺峔抸偼丆
壓棳懁偺晹暘栘偐傜嵞峔抸偡傞張棟傪峴偊偽傛偄偙偲偑暘偐傝傑偡丅
乵僾儘僌儔儉乶
丂丂private void 僸乕僾壔(ref int[] a, int
嵍, int 塃)
丂丂{
丂丂丂丂int AA = a[嵍];丂int 巕; int
恊;
丂丂丂丂for(恊 = 嵍; 恊 < (塃 + 1)/2 ;
恊 = 巕)
丂丂丂丂{
丂丂丂丂丂丂int 嵍偺巕 = 恊 * 2 + 1; int
塃偺巕 = 嵍偺巕 + 1;
丂丂丂丂丂丂巕 = (塃偺巕 <= 塃 &&
a[塃偺巕]>a[嵍偺巕]) ? 塃偺巕 : 嵍偺巕;
丂丂丂丂丂丂if(AA >= a[巕]) break;
a[恊]=a[巕];
丂丂丂丂}
丂丂丂丂a[恊]=AA;
丂丂}
丂丂private void 僸乕僾僜乕僩()
丂丂{
丂丂丂丂int i;
丂丂丂丂for (i = (Data.Length - 1) / 2;i
>= 0; i--)
丂丂丂丂丂丂 僸乕僾壔(ref Data, i, Data.Length
- 1);
丂丂丂丂for (i = Data.Length - 1 ;i >
0; i--)
丂丂丂丂{
丂丂丂丂丂丂丂swap(ref Data[0], ref
Data[i]);
丂丂丂丂丂丂丂僸乕僾壔(ref Data, 0, i-1);
丂丂丂丂}
丂丂}
   
 1. 婎杮揑側傾儖僑儕僘儉 1. 婎杮揑側傾儖僑儕僘儉
 2. 婎杮揑側僨乕僞峔憿 2. 婎杮揑側僨乕僞峔憿
 3. 憖嶌傪敽偆僨乕僞峔憿 3. 憖嶌傪敽偆僨乕僞峔憿
 4. 扵嶕 4. 扵嶕
 5. 嵞婣揑傾儖僑儕僘儉 5. 嵞婣揑傾儖僑儕僘儉
 6. 僜乕僩 6. 僜乕僩
 7. 廤崌 7. 廤崌
 8. 暥帤楍張棟 8. 暥帤楍張棟
 9. 怓乆側傾儖僑儕僘儉 9. 怓乆側傾儖僑儕僘儉

忋偺僞僀僩儖傪僋儕僢僋偟傑偡
|

 丂6丏8 僸乕僾僜乕僩
丂6丏8 僸乕僾僜乕僩





