パーソナル

　2．４構造体

番号	以下をクリックすると同位置にジャンプします
（１）	構造体の考え方
（２）	構造体の配列
（３）	構造体を使った演算子の定義
（４）	複素数演算子を使ったプログラム例

（１）構造体の考え方

あるグループの身長と体重が得られたものとして
例えば，統計分析等を行うときのデータ構造を考えてみましょう。

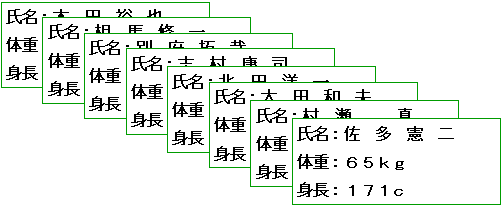
氏名（文字列）	体重（浮動小数点）	身長（浮動小数点）
佐　多　憲　二	65	171
村　瀬　真　吾	57	169
大　田　和　夫	60	168
北　田　洋　一	73	172
志　村　康　司	62	170
別　府　拓　哉	59	167
相　馬　修　一	68	176
木　田　裕　也	61	167

それぞれ次のように別々の配列で表現することができます。
　　
　　private string[ ] 氏名=new string[8];
　　private double[ ] 体重=new double[8];
　　private double[ ] 身長=new double[8];

これらのデータ間の関係は，プログラムを作った人は意識していても，
プログラム上は，直接関係付けられていません。

一方，プログラム内で次のようなカード形式に似た形で表現できれば，
氏名，体重，身長がひとまとまりのデータであることが
直接分かるような表現になります。

　　　
　　　　　図２－１０　体格データの集まり

そこで，異なるデータの型でもひとまとまりのデータとして扱う方法，
これが構造体です。まず，以下のように構造体の宣言を行います。

　　public struct 体格データ
　　{
　　　　public string 氏名;
　　　　public double 体重;
　　　　public double 身長;
　　}

ここで，上記の構造体は以下の意味を持ちます。

　　(a) 体格データ
　　　　「体格データ」という型名。構造体タグ（structure tag）と呼ぶ。
　　　　（CやC++では，「struct 体格データ」が型名になるが，
　　　　　C#では，型名は「体格データ」となるので要注意）

　　(b) 氏名，体重，身長
　　　　構造体の要素。構造体メンバ（structure member）と呼ぶ。
　　　　なお，たまたま構造体メンバの型がすべて同じでもかまわない。

データを使うためには，まず，通常の変数の型宣言と同じように
以下のように宣言して使います。

　　　体格データ X;

参照したり，設定するときは，次のようにドット（．）をつけて
構造体メンバ名を指定します。

　　　X.氏名=textBox1.Text;
　　　X.体重=double.Parse(textBox2.Text);
　　　X.身長=double.Parse(textBox3.Text);

この表現は，オブジェクトとプロパティの関係と同じです。

プログラム例として，体格データを入力して，
肥満度を計算するプログラムを示します。

標準体重計算は，有名なＢＭＩで行います。

［Program 2－14］肥満度の計算

　　　　　　

　　　　　

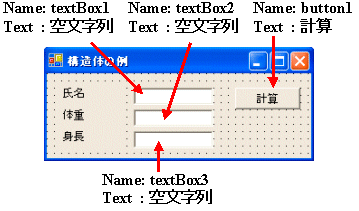
public struct 体格データ
{
　　public string 氏名;
　　public double 体重,身長;
}
public class Form1 : System.Windows.Forms.Form
{　　・
　　・
　　・
　　private void button1_Click(object sender, System.EventArgs e)
　　{
　　　　体格データ X;string S;
　　　　X.氏名=textBox1.Text;
　　　　X.体重=double.Parse(textBox2.Text);
　　　　X.身長=double.Parse(textBox3.Text);
　　　　double 標準体重=X.身長*X.身長*22/10000;
　　　double 肥満度=(X.体重-標準体重)/標準体重;
　　　　if(肥満度>=0.1)　　　 S=“太りすぎ”;
　　　else if(肥満度<=-0.1) S=“やせすぎ”;
　　　　else　　　　　　　　　 S="標準";
　　　　MessageBox.Show(X.氏名 +“さんは，” + S + “です。肥満度 = ”
　　　　　　　　　　 + 肥満度.ToString("#0.00"));
　　}
}

番号	以下をクリックすると同位置にジャンプします
（１）	構造体の考え方
（２）	構造体の配列
（３）	構造体を使った演算子の定義
（４）	複素数演算子を使ったプログラム例

（２）構造体の配列

構造体も配列として扱うことができます。たとえば，以下のように宣言します。

　　 private 体格データ[ ] Z=new 体格データ[8]

代入や参照では，

　　構造体の配列名[インデックス].構造体メンバ名

として指定します。

[例]
　　Z[2].氏名=“大　田　和　夫”;
　　Z[2].体重=60;
　　Z[2].身長=168;

例として，身長や体重の平均値を求めるプログラムを示します。

［Program 2－15］身長や体重の平均値

　　

（体格データの構造体宣言は，[Program 2-14]と同じ）　　　　

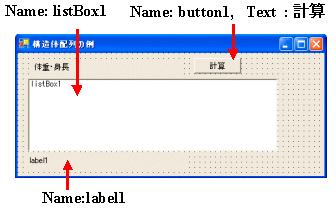
private 体格データ[] Z=new 体格データ[8];

private void button1_Click(object sender, System.EventArgs e)
{
　　double T1=0;double T2=0;
　 for(int i=0;i<Z.Length;i++) { T1 += Z[i].体重;T2 += Z[i].身長; }
　　T1=T1/Z.Length; T2=T2/Z.Length;
　　label1.Text=" 平均体重 = "+T1.ToString() +" 平均身長 = "+T2.ToString();
}
private void Form1_Load(object sender, System.EventArgs e)
{
　　Z[0].氏名="佐　多　憲　二"; Z[0].体重=65; Z[0].身長=171;
　　Z[1].氏名="村　瀬　　　真"; Z[1].体重=57; Z[1].身長=169;
　　Z[2].氏名="大　田　和　夫"; Z[2].体重=60; Z[2].身長=168;
　　Z[3].氏名="北　田　洋　一"; Z[3].体重=73; Z[3].身長=172;
　　Z[4].氏名="志　村　康　司"; Z[4].体重=62; Z[4].身長=170;
　　Z[5].氏名="別　府　拓　哉"; Z[5].体重=59; Z[5].身長=167;
　　Z[6].氏名="相　馬　修　一"; Z[6].体重=68; Z[6].身長=176;
　　Z[7].氏名="木　田　裕　也"; Z[7].体重=61; Z[7].身長=167;
　　for(int i=0;i<Z.Length;i++)
　　　listBox1.Items.Add(Z[i].氏名+": 体重 = " +Z[i].体重+"kg 身長 = "+Z[i].身長);
　　label1.Text="";
}

番号	以下をクリックすると同位置にジャンプします
（１）	構造体の考え方
（２）	構造体の配列
（３）	構造体を使った演算子の定義
（４）	複素数演算子を使ったプログラム例

（３）構造体を使った演算子の定義

構造体は，ユーザが定義したデータ型と考えることができます。
新しいデータ型を定義したら，そのデータ型に対する演算を
考えることができます。

この演算で通常の数値と同じような演算子を使うことができれば，
プログラムは非常に分かりやすくなります。

例として，複素数を考えてみましょう。

複素数は，実部と虚部に分けることができますので，
例えば，次のように構造体として表現できます。

　　public struct Complex
　　{
　　　　 public double R;　// 実部
　　　　public double I;　 // 虚部
　 }

ここで，たとえば，

　　Complex A, B, C, D；
　　D = (A + B) *D ;
　　

等と表現できると非常に便利です。

演算子の定義を示す前に，複素数演算について整理しておきます。

■基本的な複素数演算

■複素数の逆数

除算を導入する前に逆数を考えてみましょう。

除算は，除数の逆数に被除数を乗算することに帰着します。

■複素数の平方根

２乗する前の実数部，虚数部を，２乗した結果の実数部，虚数部で
表すことを試みます。
まず，

ここで，
　　　　

ですから，

として実数部と虚数部を求めることができます。
通常,平方根では，正の値のみを有効にします。

■複素数の指数

ですから

として計算できます。

■その他

この他，複素数が等値（==）は，差の絶対値が微小な値以下であること
で判定します。

なお，等値を定義しても

　　「EqualsおよびGetHashCodeはオーバーライドされません」

とのワーニングエラー（軽度のエラー）が表示されます。
実行に影響はありませんが，目障りですので，

これらの関数のオーバーライドを定義しておきます。

［Program 2－16］複素数演算子定義
　　　

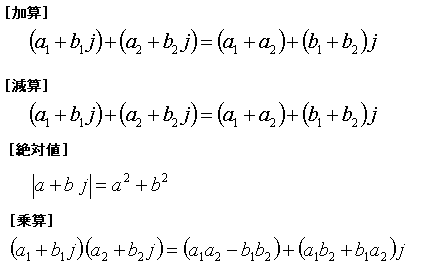
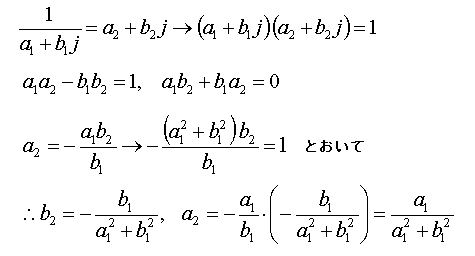
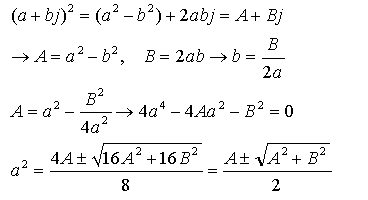
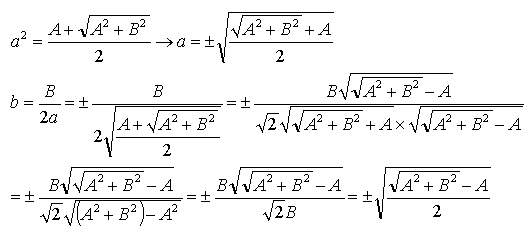
public struct Complex
{
　public double R; // 実部
　public double I; // 虚部
　public Complex(double P1,double P2) { this.R=P1; this.I=P2; }
　// 加算
　public static Complex operator +(Complex a,Complex b)
　　　　{ return new Complex(a.R+b.R,a.I+b.I); }
　public static Complex operator +(double a,Complex b)
　　　　{ return new Complex(a+b.R, b.I); }
　public static Complex operator +(Complex a,double b)
　　　　{ return new Complex(a.R+b, a.I); }
　public static Complex operator +(Complex b)
　　　　{ return new Complex(b.R,b.I); }
　// 減算
　public static Complex operator -(Complex b)
　　　　{ return new Complex(- b.R, - b.I); }
　public static Complex operator -(Complex a,Complex b)
　　　　{ return new Complex(a.R - b.R, a.I - b.I); }
　public static Complex operator -(double a,Complex b)
　　　　{ return new Complex(a - b.R, -b.I); }
　public static Complex operator -(Complex a,double b)
　　　　{ return new Complex(a.R - b, a.I); }
　// 乗算
　public static Complex operator *(Complex a,Complex b){
　　double X, Y; X = a.R * b.R - a.I * b.I; Y = a.R * b.I + a.I * b.R;
　　return new Complex(X,Y);
　}
　public static Complex operator *(double a,Complex b)
　{ double X, Y; X = a * b.R; Y = a * b.I; return new Complex(X,Y); }
　public static Complex operator *(Complex a,double b)
　{ double X, Y; X = a.R * b; Y = a.I * b; return new Complex(X,Y); }
　// 除算
　public static Complex operator /(Complex a,Complex b){
　　double X, Y, S; S = b.R * b.R + b.I * b.I;
　　X = b.R / S; Y = - b.I / S; Complex c=new Complex(X,Y);
　　return ( a * c );
　}
　public static Complex operator /(double a,Complex b){
　　double X, Y, S; S = b.R * b.R + b.I * b.I;
　　X = b.R / S; Y = - b.I / S; Complex c=new Complex(X,Y);
　　return ( a * c );
　}
　public static Complex operator /(Complex a,double b)
　{ return new Complex( a.R/b, a.I/b ); }
　// 等値
　public static bool operator ==(Complex a,Complex b){
　　double S1,S2; Complex c; S1 = Abs(a); S2 = Abs(b);
　　if(S1<S2) S1 = S2;
　　if (S1<0.000001) return(true);
　　c = a - b;
　　if (Abs(c) < S1*0.0000001) return(true); return(false);
　}
　public static bool operator ==(double a,Complex b){
　　if(Math.Abs(b.I) >0.0000001) return(false);
　　double c = a - b.R;
　　if (Math.Abs(c) < 0.0000001) return(true); return(false);
　}
　public static bool operator ==(Complex a,double b){
　　if(Math.Abs(a.I) >0.0000001) return(false);
　　double c = a.R - b;
　　if (Math.Abs(c) < 0.0000001) return(true); return(false);
　}
　// 不等値
　public static bool operator !=(Complex a,Complex b){return (!(a==b));}
　public static bool operator !=(double a,Complex b) {return (!(a==b));}
　public static bool operator !=(Complex a,double b) {return (!(a==b));}
　// 絶対値
　public static double Abs(Complex a){return (a.R * a.R + a.I * a.I);}
　// 平方根
　public static Complex Sqrt(Complex a) {
　　double SS=Math.Sqrt(a.R*a.R+a.I*a.I);
　　return new Complex( Math.Sqrt((SS+a.R)/2),Math.Sqrt((SS-a.R)/2) );
　}
　// 指数
　public static Complex Exp(Complex a){
　　double EP=Math.Exp(a.R);double TH=a.I;
　　return new Complex( Math.Cos(TH)*EP, Math.Sin(TH)*EP );
　}
　// 文字列化
　public override string ToString( ) {
　　if (R==0) return(I.ToString()+" j");
　　if (I<0) return("( "+R.ToString()+" - " + (-I).ToString() +" j )");
　　return("( "+R.ToString()+" + " + I.ToString() +" j )");
　}
　// 以下，ワーニングエラーなしにするためのオーバーライド
　public override bool Equals(Object obj)
　{
　　//Check for null and compare run-time types.
　　if (obj == null || GetType() != obj.GetType()) return false;
　　Complex p = (Complex)obj;
　　return (R == p.R) && (I == p.I);
　}
　public override int GetHashCode() { return (int)R ^ (int)I; } }

番号	以下をクリックすると同位置にジャンプします
（１）	構造体の考え方
（２）	構造体の配列
（３）	構造体を使った演算子の定義
（４）	複素数演算子を使ったプログラム例

（４）複素数演算子を使ったプログラム例

演算子定義が正しいことを確認するためのプログラムを
例題として示します。

［Program 2－17］複素数演算子を使った例
　　　　
　　　

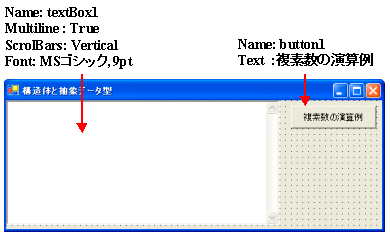
private void button1_Click(object sender, System.EventArgs e)
{
　string S="";
　Complex A=new Complex(5,6); S = S + "\r\n A = " + A.ToString();
　Complex B=new Complex(3,4); S = S + "\r\n B = " + B.ToString();
　Complex X=new Complex(2,0); S = S + "\r\n X = " + X.ToString();
　double C=2; 　　　S = S + "\r\n C = " + C.ToString();

　Complex D; D=A+B; S = S + "\r\n\r\n A + B = " + D.ToString();
　D=A + C; S = S + "\r\n A + C = " + D.ToString();
　D=C + A; S = S + "\r\n C + A = " + D.ToString();

　D=A-B; S = S + "\r\n\r\n A - B = " + D.ToString();
　D=A - C; S = S + "\r\n A - C = " + D.ToString();
　D=C - A; S = S + "\r\n C - A = " + D.ToString();

　D=A*B; S = S + "\r\n\r\n A * B = " + D.ToString();
　D=A * C; S = S + "\r\n A * C = " + D.ToString();
　D=C * A; S = S + "\r\n C * A = " + D.ToString();

　D=A/B; S = S + "\r\n\r\n A / B = " + D.ToString();
　D=A / C; S = S + "\r\n A / C = " + D.ToString();
　D=C / A; S = S + "\r\n C / A = " + D.ToString();

　bool E;
　E = A == B; S = S + "\r\n\r\n A == B = " + E.ToString();
　E = A == C; S = S + "\r\n A == C = " + E.ToString();
　E = C == A; S = S + "\r\n C == A = " + E.ToString();
　E = X == B; S = S + "\r\n\r\n X == B = " + E.ToString();
　E = X == C; S = S + "\r\n X == C = " + E.ToString();
　E = C == X; S = S + "\r\n C == X = " + E.ToString();

　E = A != B; S = S + "\r\n\r\n A != B = " + E.ToString();
　E = A != C; S = S + "\r\n A != C = " + E.ToString();
　E = C != A; S = S + "\r\n C != A = " + E.ToString();
　E = X != B; S = S + "\r\n\r\n X != B = " + E.ToString();
　E = X != C; S = S + "\r\n X != C = " + E.ToString();
　E = C != X; S = S + "\r\n C != X = " + E.ToString();

　Complex Y;
　Y=(A/B)*B; S = S + "\r\n\r\n (A / B) * B = " + Y.ToString();
　Y=(C/A)*A; S = S + "\r\n (C / A) * A = " + Y.ToString();
　Y=Complex.Sqrt(A); S = S + "\r\n Sqrt(A) = " + Y.ToString();
　
Y=Y*Y; S = S + "\r\n Sqrt(A)*Sqrt(A) = " + Y.ToString();

　Y=Complex.Exp(new Complex(0,Math.PI/6));
　S = S + "\r\n Exp(πj/6) = " + Y.ToString();
　textBox1.Text=S;
}

番号	以下をクリックすると同位置にジャンプします
（１）	構造体の考え方
（２）	構造体の配列
（３）	構造体を使った演算子の定義
（４）	複素数演算子を使ったプログラム例

1. 基本的なアルゴリズム

 2. 基本的なデータ構造

 3. 操作を伴うデータ構造

 4. 探索

 5. 再帰的アルゴリズム

 6. ソート

 7. 集合

 8. 文字列処理

 9. 色々なアルゴリズム

上のタイトルをクリックします